You can analyze circuits with dependent sources using node-voltage analysis, source transformation, and the Thévenin technique, among others. For analyzing circuits that have dependent sources, each technique has particular advantages.
Utilize node-voltage analysis to analyze circuits with dependent sources
Using node voltage methods to analyze circuits with dependent sources follows much the same approach as for independent sources. Consider the circuit shown here. What is the relationship between the output voltage vo and is?
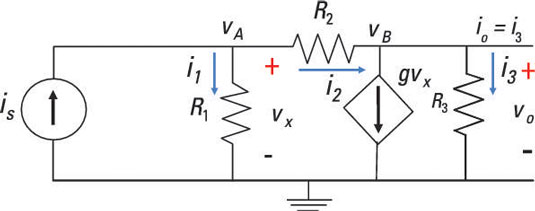
The first step is to label the nodes. Here, the bottom node is your reference node, and you have Node A (with voltage vA) at the upper left and Node B (with voltage vB) at the upper right. Now you can formulate the node voltage equations.
Using node-voltage analysis involves Kirchhoff’s current law (KCL), which says the sum of the incoming currents is equal to the sum of the outgoing currents. At Node A, use KCL and substitute in the current expressions from Ohm’s law (i = v/R). The voltage of each device is the difference in node voltages, so you get the following:
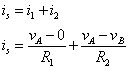
Rearranging gives you the node voltage equation:
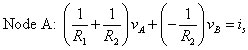
At Node B, again apply KCL and plug in the current expressions from Ohm’s law:
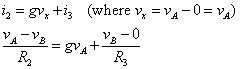
Rearranging the preceding equation gives you the following node voltage equation at Node B:
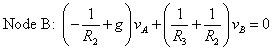
The two node voltage equations give you a system of linear equations. Put the node voltage equations in matrix form:
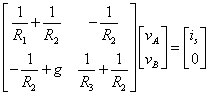
You can solve for the unknown node voltages vA and vB using matrix software. After you have the node voltages, you can set the output voltage vo equal to vB. You can then use the ever-faithful Ohm’s law to find the output current io:
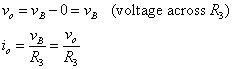
Utilize source transformation to analyze circuits with dependent sources
To see the source transformation technique for circuits with dependent circuits, consider Circuit A as shown here.
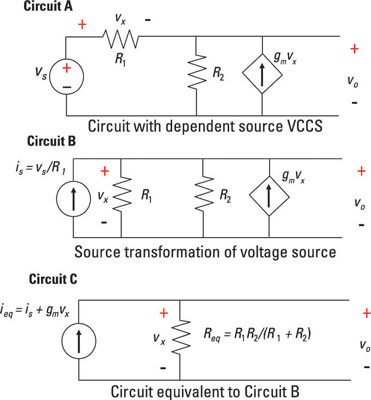
Suppose you want to find the voltage across resistor R3. To do so, you can perform a source transformation, changing Circuit A (with an independent voltage source) to Circuit B (with an independent current source). You now have all the devices connected in parallel, including the dependent and independent current sources.
Don’t use source transformation for dependent sources, because you may end up changing or losing the dependency. You need to make sure the dependent source is a function of the independent source.
Here’s the equation for the voltage source and current source transformation:
The independent current source is and the dependent current source gvx point in the same direction, so you can add these two current sources to get the total current ieq going through the resistor combination R1 and R2. The total current ieq is ieq = is + gmvx. Because vx is the voltage across R2, vx is also equal to vo in Circuit B: vo = vx.
Resistors R1 and R2 are connected in parallel, giving you an equivalent resistance Req:
The output voltage is equal to the voltage across Req, using Ohm’s law and ieq. You see the equivalent circuit with ieq and Req in Circuit C. Because the dependent current source is dependent on vx, you need to replace the voltage vx with vo:
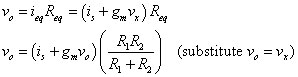
Solving for the output voltage vo gives you
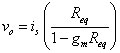
See how the output voltage is a function of the input source? The final expression of the output should not have a dependent variable.
Utilize the Thévenin technique to analyze circuits with dependent sources
The Thévenin approach reduces a complex circuit to one with a single voltage source and a single resistor. Independent sources must be turned on because the dependent source relies on the excitation due to an independent source.
To find the Thévenin equivalent for a circuit, you need to find the open-circuit voltage and the short-circuit current at the interface. In other words, you need to find the i-v relationship at the interface.
To see how to get the Thévenin equivalent for a circuit having a dependent source, look at this example. It shows how to find the input resistance and the output Thévenin equivalent circuit at interface points A and B.
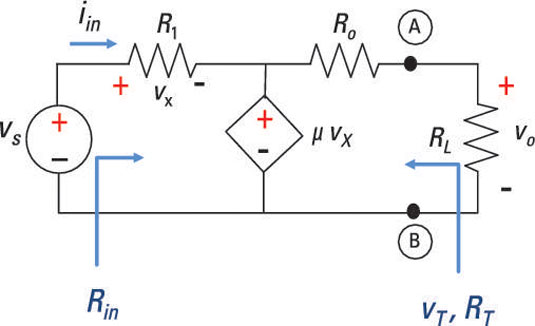
The input resistance is
Using Ohm’s law, the current iin through R1 is
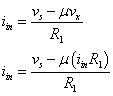
Solving for iin, you wind up with
Substituting iin into the input-resistance equation gives you
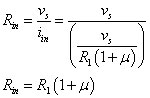
Here, the dependent source increases the input resistance by approximately multiplying the resistor R1 by the dependent parameter μ. R1 is the input resistance without the dependent source. To find the Thévenin voltage vT and the Thévenin resistance RT, you have to find the open-circuit voltage voc and short-circuit current isc. The resistance RT is given by the following relationship:
Based on the sample circuit, the open-circuit voltage is voc = μvx. You find that the short-circuit current gives you
After finding voc and isc, you find the Thévenin resistance:
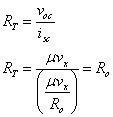
The output resistance Ro and Thévenin resistance RT are equal. Based on Kirchhoff’s voltage law (KVL), you have the following expression for vx:
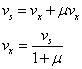
Substituting vx into the equation for the open-circuit voltage voc, you wind up with
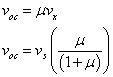
The open-circuit voltage, voc, equals the Thévenin voltage, vT. The nitty-gritty analysis leaves you with Thévenin voltage vT and Thévenin resistance RT, entailing a dependent voltage gain of μ:
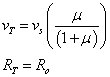
When μ is very large, the Thévenin voltage vT equals the source voltage vs.

