This relationship makes sense if you think about pressure in terms of kinetic molecular theory. Adding a gaseous sample into a particular volume that already contains other gases increases the number of particles in that space. Because pressure depends on the number of particles colliding with the container walls, increasing the number of particles increases the pressure proportionally.
There's no one specific pressure unit you have to use when doing problems with Dalton's partial-pressures equation. As long as the pressure units for all the gases are the same, you're good to go. However, if all the pressures given aren't in the same units, then some conversion must take place!
Here's an example: A chemist designs an experiment to study the chemistry of the atmosphere of the early Earth. She constructs an apparatus to combine pure samples of the primary volcanic gases that made up the atmosphere billions of years ago: carbon dioxide, ammonia, and water vapor. If the partial pressures of these gases are 50 kPa, 80 kPa, and 120 kPa, respectively, what's the pressure of the resulting mixture?However difficult early-Earth atmospheric chemistry may prove to be, this particular problem is a simple one. Dalton's law states that the total pressure is simply the sum of the partial pressures of the component gases:
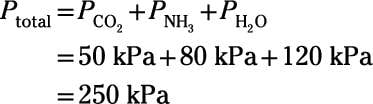
So, the pressure of the resulting mix is 250 kPa.
Here's another problem: A chemist adds solid zinc powder to a solution of hydrochloric acid to initiate the following reaction:
The chemist inverts a test tube and immerses the open mouth into the reaction beaker to collect the hydrogen gas that bubbles up from the solution. The reaction proceeds to equilibrium. At the end of the experiment, the water levels within the tube and outside the tube are equal. The pressure in the lab is 101.325 kPa, and the temperature of all components is 298 K. The vapor pressure of water at 298 K is 3.17 kPa. What is the partial pressure of hydrogen gas trapped in the tube?
The system has come to equilibrium, so the interior of the tube contains a gaseous mixture of hydrogen gas and water vapor. Because the water levels inside and outside the tube are equal, you know that the total pressure inside the tube equals the ambient pressure of the lab, 101.325 kPa. The total pressure includes the partial pressure contributions from hydrogen gas and from water vapor. Set up an equation using Dalton's law, rearrange the equation to solve for the pressure of just the hydrogen gas, plug in your numbers, and solve:
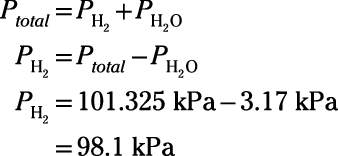
So, the partial pressure of hydrogen gas trapped in the tube is 98.1 kPa.

