The outcome of a statistical test is a decision to either accept or reject H0 (the Null Hypothesis) in favor of HAlt (the Alternate Hypothesis). Because H0 pertains to the population, it's either true or false for the population you're sampling from. You may never know what that truth is, but an objective truth is out there nonetheless.
The truth can be one of two things, and your conclusion is one of two things, so four different situations are possible; these are often portrayed in a fourfold table.
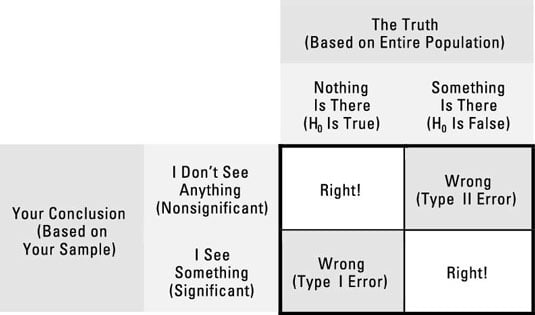
Here are the four things that can happen when you run a statistical significance test on your data (using an example of testing a drug for efficacy):
You can get a nonsignificant result when there is truly no effect present. This is correct — you don't want to claim that a drug works if it really doesn't. (See the upper-left corner of the outlined box in the figure.)
You can get a significant result when there truly is some effect present. This is correct — you do want to claim that a drug works when it really does. (See the lower-right corner of the outlined box in the figure.)
You can get a significant result when there's truly no effect present. This is a Type I error — you've been tricked by random fluctuations that made a truly worthless drug appear to be effective. (See the lower-left corner of the outlined box in the figure.)
Your company will invest millions of dollars into the further development of a drug that will eventually be shown to be worthless. Statisticians use the Greek letter alpha to represent the probability of making a Type I error.
You can get a nonsignificant result when there truly is an effect present. This is a Type II error (see the upper-right corner of the outlined box in the figure) — you've failed to see that the drug really works, perhaps because the effect was obscured by the random noise in the data.
Further development will be halted, and the miracle drug of the century will be consigned to the scrap heap, along with the Nobel prize you'll never get. Statisticians use the Greek letter beta to represent the probability of making a Type II error.
Limiting your chance of making a Type I error (falsely claiming significance) is very easy. If you don't want to make a Type I error more than 5 percent of the time, don't declare significance unless the p value is less than 0.05. That's called testing at the 0.05 alpha level.
If you're willing to make a Type I error 10 percent of the time, use p
Why not always use a small alpha level (like p
You need to strike a balance between Type I and Type II errors — between the alpha and beta error rates. If you make alpha too small, beta will become too large, and vice versa.
