You can use the law of tangents to solve for the measures of missing parts of a triangle when you have two sides of a triangle and the angle between them (referred to as SAS, or side-angle-side, in trigonometry). The law of tangents may look a bit intimidating, but it’s really quite nice.
In triangle ABC, with sides a, b, and c opposite the respective angles A, B, and C, the law of tangents states
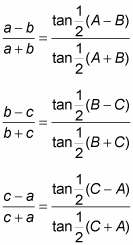
The best way to show how the law of tangents works is with an example. In triangle ABC, a is 52, b is 28, and angle C is 80 degrees. To find the remaining parts of the triangle, follow these steps:
Use the law of tangents involving sides a and b.
Fill in the values that you know and simplify.

Multiply each side by the denominator on the right.
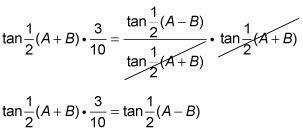
Determine A + B.
The sum of angles A and B equals 180 degrees minus the measure of angle C: A + B = 180 – 80 = 100.
Replace (A + B) with 100 and simplify.
Use a scientific calculator to do the calculations.
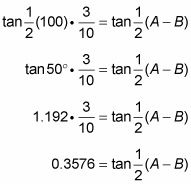
Find the value of A – B.
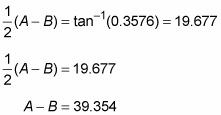
The difference between angle A and angle B is 39.354, or about 39 degrees.
Determine A and B by solving the system of equations for A + B and A – B.
Eliminate one of the variables by adding the two equations together.

Because A is 69.5, B equals 100 minus 69.5, or 30.5. Rounding these values to whole numbers, you get A = 70 and B = 30. (If you’re uncomfortable with rounding 69.5 up to 70, be aware that, if you had used 39.354 instead of the rounded version, 39, in the system of equations, you would have gotten a number closer to 70.)
Solve for side c by using the law of sines.
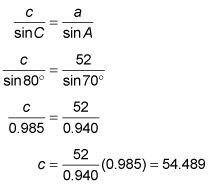
Side c is about 54 units long.

