Translating Tangent Functions on a Graph

Adding a number to a tangent function results in raising the curve on the graph by that amount. Likewise, subtracting a number drops the curve.

The tangent function raised and lowered by 3 units.

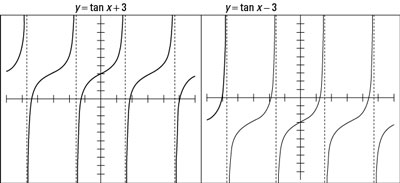
Because the tangent function has values from negative infinity to positive infinity, adding to or subtracting from the function doesn’t change what values the tangent has — it just changes where they happen. When you add or subtract, the point of inflection in the tangent curve (where the curve appears to flatten out a bit) shifts up or down. The preceding figure shows some graphs to illustrate this shift.

Adding or subtracting a number from the angle variable of the tangent function has the same effect as with the sine and cosine — it moves the curve to the left or right. The graph of y = tan (x + 1) shifts one unit to the left, including the asymptotes. The graph of y = tan (x – 1) moves everything to the right one unit. The following figure shows a comparison of the tangent function and the two shifted curves.

The tangent function moved left and right 1 unit.

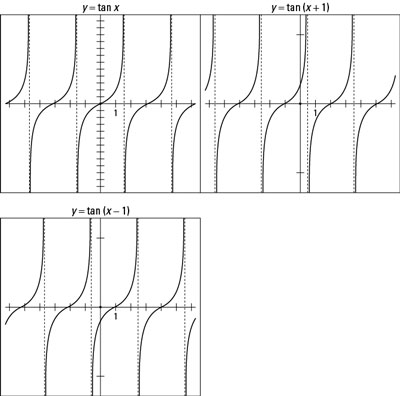
If you have a tough time telling these graphs apart, just look for the point of inflection of the tangent curve. The point of inflection is a good reference mark when looking at all these variations.