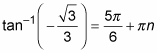Technically, an inverse trig function is supposed to have only one output for each input. (Part of the definition of an inverse is that the function and inverse are one-to-one.) With any one-to-one function, each input has one output, and each output has one input.
For all the practical uses of trig inverses, you have a way around this rule. You can designate whether you want one answer or many answers by using either the inverse function or the inverse relation. A relation is a bit looser than a function; it allows more than one output to have the same input. To differentiate between these two entities, the common practice is to use capital letters for the function and lowercase letters for the relation.
| Trig Functions | Trig Relations |
|---|---|
| Sin–1 x or Arcsin x | sin–1 x or arcsin x |
| Cos–1 x or Arccos x | cos–1 x or arccos x |
| Tan–1 x or Arctan x | tan–1 x or arctan x |
| Cot–1 x or Arccot x | cot–1 x or arccot x |
| Sec–1 x or Arcsec x | sec–1 x or arcsec x |
| Csc–1 x or Arccsc x | csc–1 x or arcscs x |
If you write the function
Just one answer exists, which is called the principal value of the inverse. But if you write
then the result can be 30 degrees, 150 degrees, 390 degrees, 510 degrees, and so on
It all depends on the situation — what you want at the time. Do you want just the principal value, or do you want multiple values? Or you may want a bunch of values within one full rotation — from 0 to 360 degrees.
When you want lots and lots of angles or answers, listing them all can be tedious. In fact, listing every possible solution may not even be doable. Rather than making a list, you can give a rule, which allows you to define an angle with all its full-rotation multiples — the angles with the same terminal side.
Let n represent any integer (. . . , –3, –2, –1, 0, 1, 2, 3, . . .). Using the n as a multiplier, you can write a long list of angles more efficiently. Instead of saying x = 30, 150, 390, 510, 750, 870, . . . , divide the list into two groups: x = 30, 390, 750, 1110; . . .; and x = 150, 510, 870, 1230; . . . ; and then use the two rules that follow:
x = 30 + 360n or x = 150 + 360n
And then, in radians, instead of saying
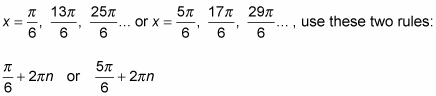
Here’s an example showing how to write all the angles that have a cosine equal to
The steps involve solving the inverse relation, not just finding the principal value for the function. Solve for the values that satisfy
List several solutions in both degrees and radians.

Write the answers in degrees by using the first two angles plus multiples of 360.
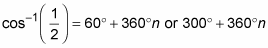
Write the answers in radians by using the first two angles plus multiples of 2π.
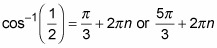
Writing all the possible angles for inverse tangent is a bit easier than writing them for sine or cosine. The tangent is positive in the first and third quadrants, which are catty-corner from one another (half a full rotation). Because of this fact, the angles that have the same function values are 180 degrees apart, and you can use nice multiples of 180 degrees or π to name all the answers. This isn’t the case with sine and cosine, though. The angles with the same function values are in quadrants that are adjacent to one another, so you have to use two separate rules — both with multiples of 360 degrees — to name all the answers.
Here’s how to write all the angles that have a tangent equal to
Solve for values that satisfy
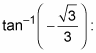
List several answers in both degrees and radians.
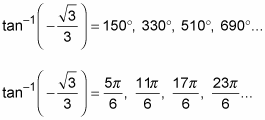
Write the answers in degrees by using multiples of 180.
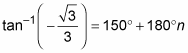
Write the answers in radians by using multiples of π.