The angles used most often in trig have trig functions with convenient exact values. Other angles don’t cooperate anywhere near as nicely as these popular ones do. A quick, easy way to memorize the exact trig-function values of the most common angles is to construct a table, starting with the sine function and working with a pattern of fractions and radicals.
Create a table with the top row listing the angles.
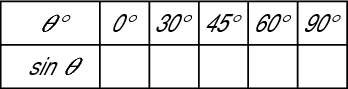
The first function, in the next row, is sine.
The entries following sin theta in the second row are the fractions and radicals with the following pattern.
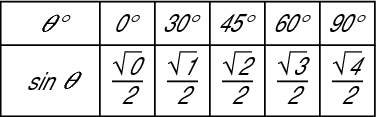
Each fraction has a denominator of 2.
The numerators of the fractions are radicals with 0, 1, 2, 3, and 4 under them, in that order.
Next, simplify the fractions that can be simplified so the table becomes what you see here.
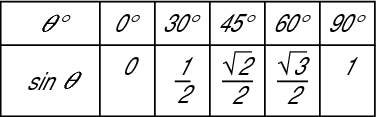
As you can see, three of the values in the second row can be simplified.
The next row, for the cosine, is just the sine’s row in reverse order.
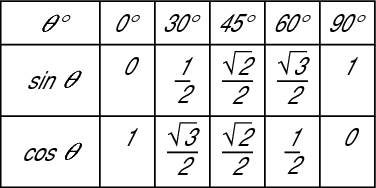
This happens because you have the angles and their complements in reverse order, too.
The next row is for the tangent. In a right triangle, you find the tangent of an acute angle with the ratio opposite/adjacent. You get the same ratio when you divide sine by cosine.
Because you already know the values for sine and cosine, you can use this property (tangent equals sine divided by cosine) to get the tangent values for the table.
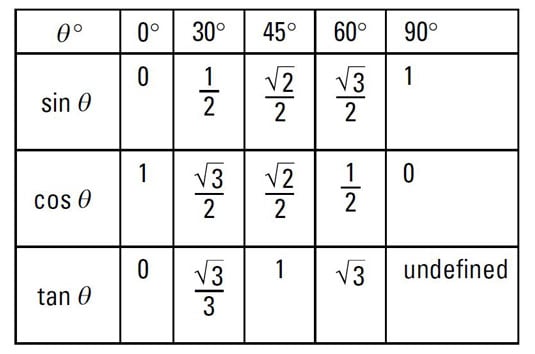
The table shows the completed table with the tangent row.

