One really efficient way of graphing the cosecant function is to first make a quick sketch of the sine function (its reciprocal). With the sine sketch in place, you can draw the asymptotes of the cosecant function through the x-intercepts (where the curve crosses the x-axis) of the sine function. You can also use the maximum and minimum values on the sine function to locate the minimum and maximum points (known as turning points) of the cosecant function.
To graph y = csc x, follow these steps:
Sketch the graph of y = sin x from –4π to 4π, as shown in this figure.
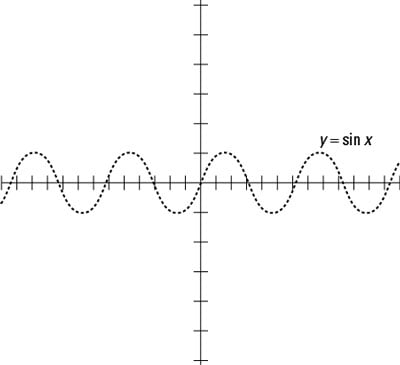 A sketch of the sine function.
A sketch of the sine function.Draw the vertical asymptotes through the x-intercepts, as the following figure shows.
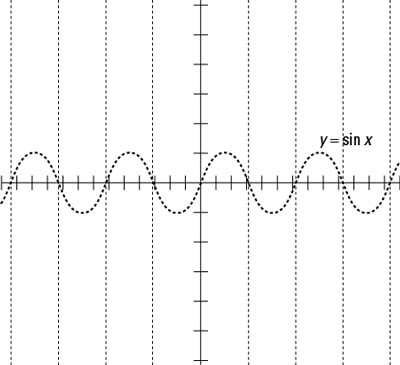 The vertical asymptotes of cosecant drawn on the graph of sine.
The vertical asymptotes of cosecant drawn on the graph of sine.Draw y = csc x between the asymptotes and down to (and up to) the sine curve, as shown in the following figure.
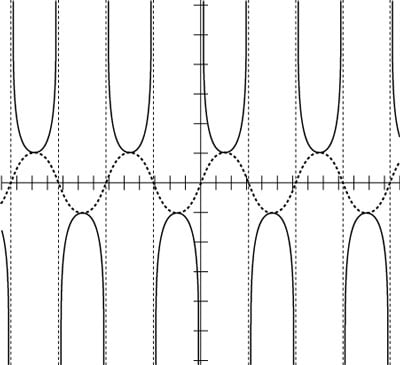 Drawing the cosecant curve by using the sine as a guide.
Drawing the cosecant curve by using the sine as a guide.The cosecant goes down to the top of the sine curve and up to the bottom of the sine curve.
After using the asymptotes and reciprocal as guides to sketch the cosecant curve, you can erase those extra lines, leaving just y = csc x. The figure that follows shows what this function looks like all on its own.
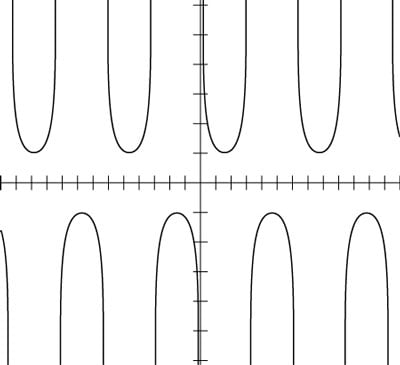 The graph of y = csc x.
The graph of y = csc x.
The range of the cosecant function includes all values equal to or greater than 1 and all values equal to or less than –1. In the preceding figure, you can see that a gap in function values lies between 1 and –1. The cosecant curve, just like all the other trig functions, keeps repeating its pattern over and over.

