A right triangle has a right angle in it. But it can only have one right angle, because the total number of degrees in a triangle is 180. If it had two right angles, then those two angles would take up all 180 degrees; no degrees would be left for a third angle. So in a right triangle, the other two angles share the remaining 90 degrees.
Right triangles can come in all sorts of shapes, but they all have that corner, where the right angle sits. You can see that in all the triangles, the right angle has the two sides that are perpendicular to one another. The other two angles are acute angles (meaning they're less than 90 degrees).
Right triangles are a familiar sight — not just in geometry classes. Carpenters have tools for measurement that are right triangles. Architects who design by hand (rather than on a computer) draw with right-triangle templates.
Even though the focus in a right triangle is the right angle, a right triangle actually has six different parts: three angles and three sides.
Now, this fact is true of any triangle, but right triangles have special names for these parts. Having special names is necessary because so many properties, theorems, and applications using right triangles are out there, and the names make talking about and explaining the triangles more clear.
The figure shows a typical right triangle labeled with capital letters and lowercase letters. Since the time of Leonard Euler, the famous Swiss mathematician, this type of labeling has been the tradition. You use lowercase letters to mark the sides of the triangle and capital letters to mark the vertex (angle) opposite the side with the corresponding lowercase letter.
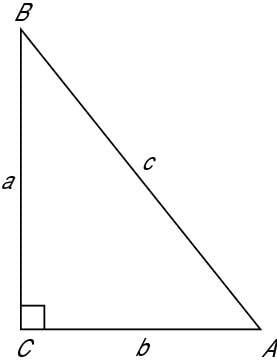
The little square at the vertex C shows that the two sides meeting there are perpendicular at that vertex — that's where the right angle is. The side c, opposite the right angle, is called the hypotenuse. The other two sides, a and b, are called the legs. The hypotenuse is always the longest side, because it's opposite the largest angle.
The angle at vertex C is the right angle, and the other two angles, A and B, are acute angles. If the measures of the angles at A and B are the same, then they're each 45 degrees, and the triangle is isosceles. If that's the case, then the lengths of the sides a and b are the same also.
If the angle at vertex A is bigger than that at vertex B, then side a is longer than side b. The measures of a triangle's angles have a direct relationship to the lengths of the sides opposite them.

