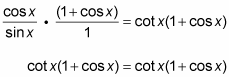With some trig identities, you may decide to simplify matters by either changing everything to sines and cosines or by factoring out some function. Sometimes, it isn’t clear which side you should work on or what you should do with either or both sides. Or you may be faced with such a conglomeration of functions that figuring out what’s going on is pretty near impossible. Another possibility is that the different terms have different powers of the same function. The technique described here takes care of a multiple number of instances.
In the following example, you can use either reciprocal or ratio identities, depending on which side you’re going to work on, to change everything to sines and cosines. Here’s how to solve the identity tan + cot = csc sec:
Replace the two terms on the left by using ratio identities.
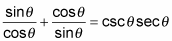
2. To get a common denominator, multiply both terms on the left by fractions equal to 1 (by using the other term’s denominator).
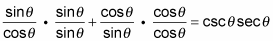
3. Simplify the fractions and then add them together, because they have a common denominator.
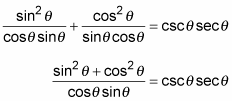
4. Replace the numerator on the left with its equivalent by using the Pythagorean identity.
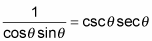
5. Use the reciprocal identities on the denominator and then flip each fraction and multiply.
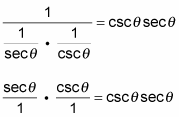
In the next example, two of the terms aren’t already written as sines, so switching those two to sines just seems natural when solving
Change the two cosecants by using the reciprocal identity.
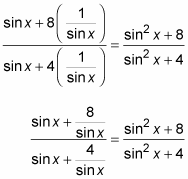
2. To eliminate the complex fractions on the left, multiply each term in the numerator and denominator by sin x. This action amounts to multiplying by sine over sine, or by 1.
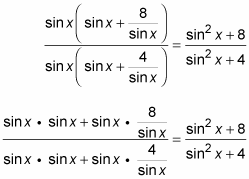
3. Simplify the numerator and denominator.
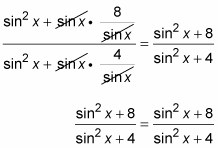
This last example has so many functions and terms in the expression that figuring out where to start almost seems impossible. Although you have other ways to approach it, one nice option is to change the fraction on the left to all sines and cosines.
Solve the identity
1. On the left side, change the secants by using the reciprocal identity and the tangents by using the ratio identity.
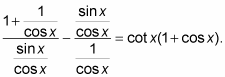
2. Multiply each term in the numerator and denominator by cos x and simplify all the terms.
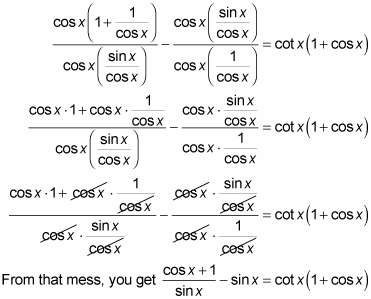
3. Find a common denominator for the two fractions on the left, add the fractions together, and simplify the result.
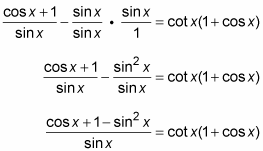
4. Now replace sin2 x with its equivalent by using the Pythagorean identity, and simplify.
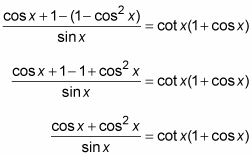
5. Factor a cos x from each term in the numerator.
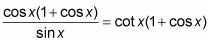
6. Finally, split the two factors in the numerator into two fractions that are multiplied by each other. Then replace
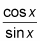
by using the ratio identity.