A trigonometric function has input values that are angles and output values that are real numbers. You have two choices when inputting values into a trig function: You can use degrees or radians. Most people are more comfortable with the degree measures, but the radian measures have a huge benefit: They’re real numbers — they have decimal values and are multiples of π.
The following are formulas for computing trig functions using the sum of the terms in a series. The more terms you use, the more accurate your answer is to more decimal places. Some of these series have recognizable formulas for the general term. Others just have a pattern that you can follow.
Sine
The sine of angle x (written in radian measure) is equal to the sum of the following terms:
The pattern seems to be to use odd-numbered factorials in the denominator, the same odd number as the power of x, and to alternate the signs. The general term for this series is
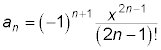
Cosine
The cosine of angle x (written in radian measure) is equal to the following terms:
This pattern uses even-numbered factorials in the denominators, the same even number as a power, and alternates signs. You may wonder about that first term. Since 0! is equal to 1 (by definition) and x0 is equal to 1, you have 1 divided by 1 which is pretty close to 1. The general term for this series is:
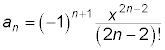
Tangent
The tangent of angle x (written in radian measure) is equal to the following terms:
The pattern here doesn’t seem all that obvious. In fact, it’s rather complicated. Instead of showing you the general term, you can actually apply the formula to find the tangent of 45 degrees, or
This is a clever choice on your part, because you already know that the tangent of 45 degrees is equal to 1.
Using the formula,
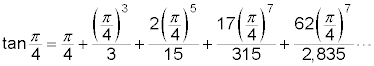
This computation will be for just the first five terms. The more terms you use, the closer to 1 you get. The next steps involve decimals and a lot of calculator computation, but bear with it:

Without getting into the gory details, you can see the individual decimal values of the terms:
Adding these five terms together, you get 1.000916. Yes, that’s greater than 1, but round up on a couple of those computations to make them all six decimal places long. Carrying more decimal places makes it more accurate, too.
Inverse tangent
The inverse tangent given a real number x gives you the angle measure from the input. The inverse tangent is equal to the following terms:
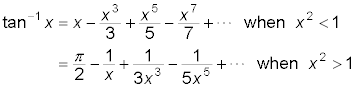
You find two different rules here. Essentially, the square of any proper fraction — any number between –1 and 1 — has a square that is less than 1.
Inverse sine
The inverse sine given a real number x between –1 and 1 (including those two numbers) gives you the angle measure from the input. The inverse sine is found with terms formed from the following formula:
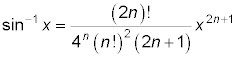
Here are the first few terms, created from the formula.
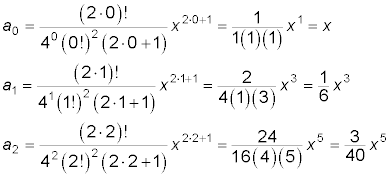
Okay. That’s enough. You get the drift.
45-degree angle
A 45-degree angle, better known as
has an infinite series that gives the value of the angle to many, many decimals places — as many as you want to compute.
The formula for all the terms is
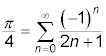
Notice that the powers of –1 make the terms alternate in sign.
Pi squared divided by 6
There are many of these goodies using powers of π in fractions that form infinite series. Here's one:
You would probably prefer using a graphing calculator to compute this angle measure, but what fun is that?
Natural log of sine
The natural logarithms are used extensively in science and business applications. Finding the natural log of the sine of angle x (given in radians) can be accomplished with the following:
You see that the only positive term in this series is the first term.
Sine as the power of e
In the previous section, you saw how to find the natural log of the sine function. The inverse of the natural log is a power of e. So, turning the tables, here’s the series for e raised to the sine of angle x (in radians).
As you can see, the signs are all over the place. And the factorials jump.
Creating 1 from sines
This last one had to be a goodie. Most people think that the number 1 is just perfect. It’s easy to compute with and a part of many mathematical structures. But if you’re bored with the normal ways of computing 1, here’s an answer to your need for stimulation:
There’s a stipulation that 0 < x < k.

