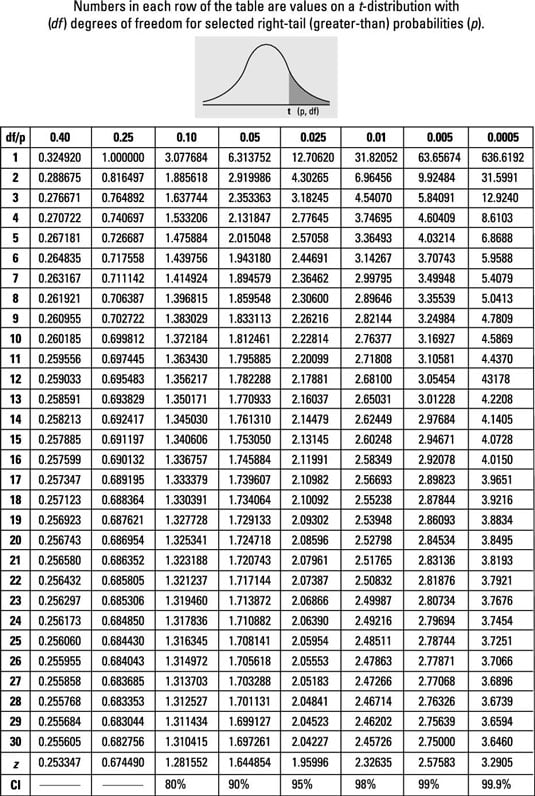
Use the t-table as needed and the following information to solve the following problems: The mean length for the population of all screws being produced by a certain factory is targeted to be
Assume that you don't know what the population standard deviation is. You draw a sample of 30 screws and calculate their mean length. The mean for your sample is 4.8, and the standard deviation of your sample (s) is 0.4 centimeters.
Sample questions
What is the 95% confidence interval for the population mean? Round your answer to two decimal places.
Answer: (4.65, 4.95)
The formula for the confidence interval for one population mean, using the t-distribution, is
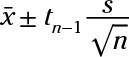
In this case, the sample mean,
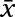
is 4.8; the sample standard deviation, s, is 0.4; the sample size, n, is 30; and the degrees of freedom, n – 1, is 29. That means tn – 1 = 2.05.
Now, plug in the numbers:
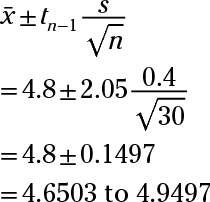
Rounded to two decimal places, the answer is 4.65 to 4.95.
What is the 90% confidence interval for the population mean? Round your answer to two decimal places.
Answer: (4.68, 4.92)
The formula for the confidence interval for one population mean, using the t-distribution, is
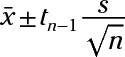
In this case, the sample mean,
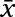
is 4.8; the sample standard deviation, s, is 0.4; the sample size, n, is 30; and the degrees of freedom, n – 1, is 29. That means that tn – 1 = 1.70.
Now plug in the numbers:
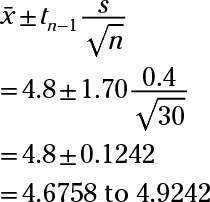
Rounded to two decimal places, the answer is 4.68 to 4.92.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

