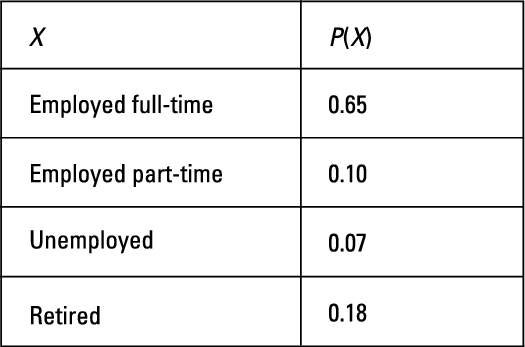
In the practice problems here, you will be finding probabilities for a random variable. The following table represents the probability distribution for X, the employment status of adults in a city.
Sample questions
If you select one adult at random from this community, what is the probability that the individual is employed part-time?
Answer: 0.10
From the table, you see that 0.10 or 10% of the adults in the city are employed part-time. Using notation, this means that P(part-time) = 0.10.
If you select one adult at random from this community, what is the probability that the individual isn't retired?
Answer: 0.82
Because total probability is always equal to 1, the probability that someone isn't retired is 1 minus the probability that the person is retired (which, according to the table, is 0.18 in this case). So the probability that the adult isn't retired is 1 – 0.18 = 0.82, or 82%. Using notation, this means that P(not retired) = 0.82.
If you select one adult at random from this community, what is the probability that the individual is working either part-time or full-time?
Answer: 0.75
Because the categories don't overlap, the probability that someone is working either part-time or full-time is the sum of their individual probabilities. You can see from the table that the probability for part-time employment is 0.10 and for full-time employment, 0.65. Add these two probabilities to get your answer: 0.10 + 0.65 = 0.75, or 75%. Using notation, this means that P(part-time or full-time) = 0.75.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

