When working on statistical problems, you sometimes will need to measure where a certain value stands in a data set by using percentiles. Creating a set of five numbers (using percentiles) can reveal some aspects of the shape, center, and variation in a data set.
Remember that a percentile isn't a percent, even though they sound the same! When used together, remember that a percentile is a cutoff value in the data set, while a percentage is the amount of data that lies below that cutoff value.
Solve the following problems about percentiles.
Sample questions
What statistic reports the relative standing of a value in a set of data?
Answer: percentile
A percentile splits the data into two parts, the percentage below the value and the percentage above the value. In other words, a percentile measures where an individual data value stands compared to the rest of the data values. For example, the 90th percentile is the value where 90% of the values lie below it and 10% of the values lie above it.
What is the statistical name for the 50th percentile?
Answer: median
The 50th percentile is the value where 50% of the data fall below it and 50% fall above it. This is the same as the definition of the median.
Your score on a test is at the 85th percentile. What does this mean?
Answer: It means that 85% of the scores were below your score and 15% of the scores were better than your score.
Percentile is the relative standing in a set of data from the lowest values to highest values. If your score is in the 85th percentile, it means that 85% of the scores are below your score and 15% are above your score.
On a multiple-choice test, your actual score was 82%, which was reported to be at the 70th percentile. What is the meaning of your test results?
Answer: It means that 70% of the students scored below you and 30% of the students scored above you and that you correctly answered 82% of the test questions.
The 70th percentile means that 70% of the scores were below your score, and 30% were above your score. Your actual score was 82%, which means that you answered 82% of the test questions correctly.
Seven students got the following exam scores (percent correct) on a science exam: 0%, 40%, 50%, 65%, 75%, 90%, 100%. Which of these exam scores is at the 50th percentile?
Answer: 65%
The 50th percentile doesn't mean a score of 50%; it's the median (or middle number) of the data set. The middle number is 65%, so that is the 50th percentile.
Students scored the following grades on a statistics test: 80, 80, 82, 84, 85, 86, 88, 90, 91, 92, 92, 94, 96, 98, 100. Calculate the score that represents the 80th percentile.
Answer: 95
A percentage score is different than a percentile. In this case, a percentage score is the percent of questions answered correctly; a percentile expresses the relative standing of a score in terms of the other scores.
Use the procedure for calculating a percentile. To calculate the kth percentile (where k is any number between 0 and 100), follow these steps:
Put all the numbers in the data set in order from smallest to largest:
80, 80, 82, 84, 85, 86, 88, 90, 91, 92, 92, 94, 96, 98, 100
Multiply k percent by the total number of values, n:
(0.80)(15) = 12
Because your result in Step 2 is a whole number, count the numbers in the data set from left to right until you reach the number you found in Step 2 (in this case, the 12th number).
The kth percentile is the average of that corresponding value in the data set and the value that directly follows it.
Find the average of the 12th and 13th numbers in the data set:
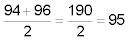
The 80th percentile is 95.
If you need more practice on this and other topics from your statistics course, visit 1,001 Statistics Practice Problems For Dummies to purchase online access to 1,001 statistics practice problems! We can help you track your performance, see where you need to study, and create customized problem sets to master your stats skills.

