A boxplot is a one-dimensional graph of numerical data based on the five-number summary. This summary includes the following statistics: the minimum value, the 25th percentile (known as Q1), the median, the 75th percentile (Q3), and the maximum value. In essence, these five descriptive statistics divide the data set into four parts, where each part contains 25% of the data.
To make a boxplot, follow these steps:
Find the five-number summary of your data set:
The minimum is the smallest value in the data set, and the maximum is the largest value in the data set. Use the following steps to find the 25th percentile (known as Q1), the 50th percentile (the median), and the 75th percentile (Q3).
Order all the values in the data set from smallest to largest.
Multiply k percent times the total number of values in the data, n.
The result is known as the index.
If the index obtained in Step 2 isn't a whole number, round it up to the nearest whole number and go to Step 4a.
If index obtained in Step 2 is a whole number, go to Step 4b.
Choose one of the following.
a. Count the values in your data set from left to right (from the smallest to the largest value) until you reach the number indicated by Step 3. The corresponding value in your data set is the kth percentile.
b. Count the values in your data set from left to right (smallest to largest) until you reach the number indicated by Step 2. The kth percentile is the average of that corresponding value in your data set and the value that directly follows it.
Create a vertical (or horizontal) number line whose scale includes the values in the five-number summary and uses appropriate units of equal distance from each other.
Mark the location of each value in the five-number summary just above the number line (for a horizontal boxplot) or just to the right of the number line (for a vertical boxplot).
Draw a box around the marks for the 25th percentile and the 75th percentile.
Draw a line in the box where the median is located.
Determine whether or not outliers are present.
To make this determination, calculate the Interquartile Range (IQR), which is found by subtracting Q3 – Q1; then multiply IQR by 1.5. Add this amount to the value of Q3 and subtract this amount from Q1. This gives you a wider boundary around the median than the box does. Any data points that fall outside this boundary are determined to be outliers.
If there are no outliers (according to your results of Step 6), draw lines from the upper and lower edges of the box out to the minimum and maximum values in the data set.
If there are outliers (according to your results of Step 6), indicate their location on the boxplot with * signs.
Instead of drawing a line from the edge of the box all the way to the most extreme outlier, stop the line at the last data value that isn't an outlier.
Many if not most software packages indicate outliers in a data set by using an asterisk (*) or star symbol and use the procedure outlined in Step 6 to identify outliers. However, not all packages use these symbols and procedures; check to see what your package does before analyzing your data with a boxplot.
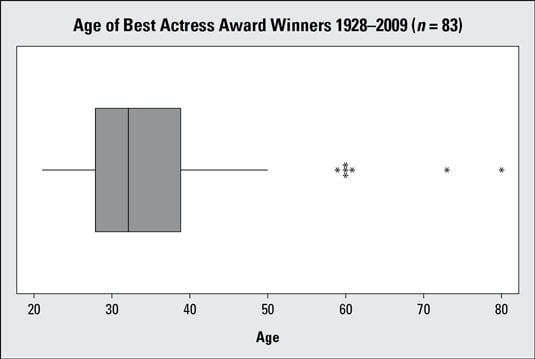
A horizontal boxplot for ages of the Best Actress Academy Award winners from 1928–2009 is shown in the above figure. You can see the numbers separating sections of the boxplot match the five-number summary statistics shown in the following figure.

Boxplots can be vertical (straight up and down) with the values on the axis going from bottom (lowest) to top (highest); or they can be horizontal, with the values on the axis going from left (lowest) to right (highest).
The steps shown here demonstrate one way of calculating the median and quartiles of the five-number summary and of constructing the boxplot. But there are several other acceptable methods. Do not be too alarmed if your calculator or a friend gives you a boxplot close to but different from what these steps would give.

