For example, say that you have a new 60-gallon aquarium and want to stock it with tetras and marbled headstanders. Each tetra requires two gallons of water, and each headstander requires four gallons of water. You need at least seven headstanders, because they tend to fight in small groups. You want at least four tetras so they’ll have nice company. The tetras cost $6 each, and the headstanders cost $5 each; you have a budget dictating that you’ll spend no more than $120 on the fish. What is the maximum number of fish you can put in your new tank?
To solve this problem, you set up a linear programming problem, following these steps.
- Choose variables to represent the quantities involved. Let t represent the number of tetras and h represent the number of headstanders.
- Write an expression for the objective function using the variables. You want the largest number of fish possible, so you’re looking for the maximum. Maximize: t + h
- Write constraints in terms of inequalities using the variables.
Use the information given in the problem.
- Because each tetra requires two gallons of water, and each headstander requires four gallons of water, and you’re limited by a 60-gallon aquarium, you have 2t + 4h ≤ 60
- You need at least seven headstanders: h ≥ 7
- You want at least four tetras: t ≥ 4
- Finally, the tetras cost $6 each, and the headstanders cost $5 each, and you can spend no more than $120 on the fish, so that means 6t + 5h ≤ 20
- Graph the feasible region using the constraint statements.
Graph the system of inequalities. In the next figure you see the lines representing the constraints and the shading representing greater than or less than.
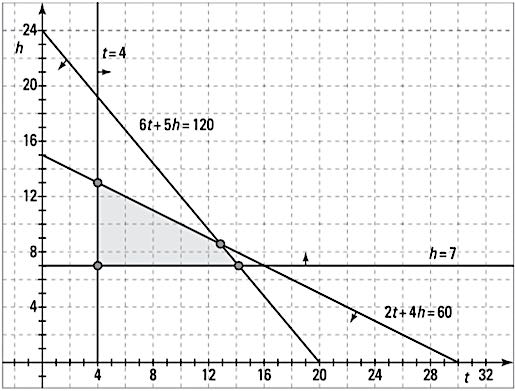 Graphing the constraints.
Graphing the constraints. - Identify the corner points of the feasible region.
The corner points are at the intersections of the four lines and are indicated in the following figure.
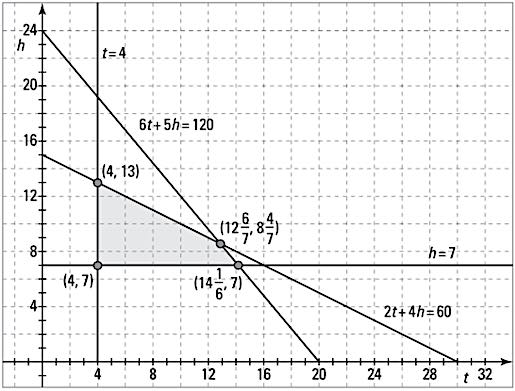 The four corner points are the candidates for the answer.
The four corner points are the candidates for the answer.- Intersection of t = 4 and h = 7: (4, 7)
- Intersection of t = 4 and 2t + 4h = 60: (4, 13)
- Intersection of 6t + 5h = 120 and 2t + 4h = 60:
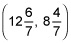
- Intersection of 6t + 5h = 120 and h = 7:
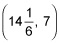
- Find and compare the values at the corner points to determine the solution.
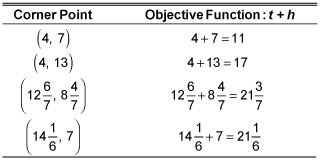
The greatest value is
but that would involve fractions of fish. You don’t want to do that, so you round each number back and make it 12 tetras and 8 headstanders, a total of 20 fish. Looking at the “runner up,” you round back to 14 tetras and 7 headstanders, a total of 21 fish. Now the choice is yours—which fish do you prefer?

