Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonYou may think that you’re “not in Kansas anymore” when you leave the familiar world of right triangles and Mr. Pythagoras to enter this new world of oblique triangles. Trigonometry allows for some calculations that aren’t possible with the geometric formulas and other types of measurement. The Law of Sines and Law of Cosines are relationships between the sides and angles of triangles that aren’t right triangles.
The applications you can solve using these new laws are many and varied. Whole new worlds are opened to you now that you don’t have triangle-type restrictions. The biggest challenge is in deciding which law to use, but even that is pretty straightforward.
You’ll work on solving for parts of triangles in the following ways:
Using the Law of Sines and choosing the pair of ratios
Applying the Law of Cosines and determining which version works
Working with the ambiguous case and deciding which angle applies
Finding the missing values of sides and angles of a triangle
Computing areas of triangles by using a formula involving a trig function
Using Heron’s formula for the area of a triangle
Practicing with practical applications
Don’t let common mistakes trip you up; keep in mind that when working with these formulas for triangles, some challenges will include
Choosing the correct pair of ratios when using the Law of Sines
Performing the order of operations correctly when applying the Law of Cosines
Identifying the correct parts of the triangle when finding the area
Writing the correct relationships between triangle parts when working on applications
Practice problems
Use the Law of Sines to find the indicated side. Round your answer to the nearest tenth.
![[Credit: Illustration by Thomson Digital]](https://www.dummies.com/wp-content/uploads/455389.image0.jpg) Credit: Illustration by Thomson Digital
Credit: Illustration by Thomson DigitalFind c.
Answer: 16.4
You know two angles and a consecutive side, so this is an angle-angle-side (AAS) problem. Find the missing side by using the Law of Sines,
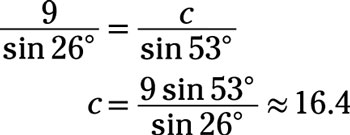
Use the Law of Sines to solve the problem:
A 14-foot pole is leaning. A wire attached to the top of the pole is anchored in the ground. The wire is 14.5 feet long and makes a 74.2-degree angle with the ground. What angle does the pole make with the ground? Round your answer to the nearest tenth of a degree.
Answer: 85.3 degrees
Always start by drawing and labeling a diagram to represent the problem:
![[Credit: Illustration by Thomson Digital]](https://www.dummies.com/wp-content/uploads/455391.image2.jpg) Credit: Illustration by Thomson Digital
Credit: Illustration by Thomson DigitalYou can see from the diagram that you know two sides and a consecutive angle, so this is a side-side-angle (SSA) problem. You know the lengths of sides a and b, and you need to find the measure of angle A. Use the Law of Sines:
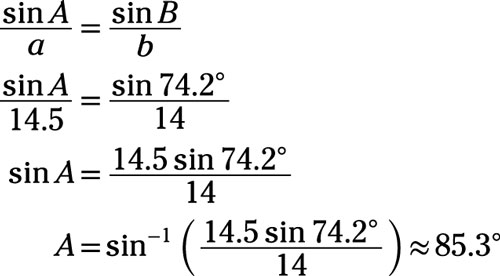
The pole makes an angle of about 85.3 degrees with the ground.

