Systems of Inequalities in Pre-Calculus

A system of inequalities has an infinite number of solutions (unless it has none at all). You solve these systems using graphs of the separate statements.

The techniques for solving these systems involve algebraic manipulation and/or matrices and matrix mathematics. When you’re solving your own systems, the approach you use is up to you.

You’ll work on solving and graphing systems of inequalities

Practice problems

1. Graph the system of inequalities.

   

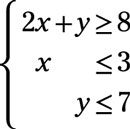
   Answer:

   

   Credit: Illustration by Thomson Digital

   To graph

   

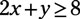
   first graph the line 2x + y = 8 (or y = –2x + 8 in slope-intercept form). Choose a test point to determine which side of the line to shade. Using (0, 0) as a test point,

   

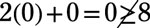
   so shade the area above and to the right of the line.

   Then graph the line x = 3. Shade to the left of the line. Finally, graph the line y = 7 and shade below that line.

   The solution is the intersection of the three shadings.

2. Graph the system of inequalities.

   

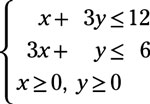
   Answer:

   

   Credit: Illustration by Thomson Digital

   To graph

   

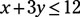
   first graph the line x = 3y = 12 (or as follows in slope-intercept form):

   

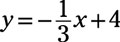
   Choose a test point to determine which side of the line to shade. Using (0, 0) as a test point,

   

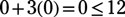
   so shade the area below and to left of the line.

   Next, graph the line 3x + y = 6 (or y = –3x + 6). Choose a test point to determine which side of the line to shade. Using (0, 0) as a test point,

   

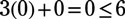
   so shade the area below and to left of the line.

   Then graph the line x = 0 (the y-axis) and the line y = 0 (the x-axis). The solution will contain only points in the first quadrant and on those axes adjacent to the first quadrant.

   The solution is the intersection of the shadings.