Pre-Calculus: 1001 Practice Problems For Dummies (+ Free Online Practice)
Explore Book Buy On AmazonIn pre-calculus and in calculus, certain polynomial functions have non-real roots in addition to real roots (and some of the more complicated functions have all imaginary roots). When you must find both, start off by finding the real roots, using techniques such as synthetic division. If you’re lucky, you’re left with a depressed quadratic polynomial to solve that’s unsolvable using real number answers. No fear! You just have to use the quadratic formula, through which you’ll end up with a negative number under the square root sign. Therefore, you express the answer as a complex number.
For instance, the polynomial g(x) = x4 + x3 – 3x2 + 7x – 6 has non-real roots. Follow these basic steps to find all the roots for this (or any) polynomial:
Classify the real roots as positive and negative by using Descartes’s rule of signs.
Three changes of sign in the g(x) function reveals you could have three or one positive real root. One change in sign in the g(–x) function reveals that you have one negative real root.
Find how many roots are possibly imaginary by using the fundamental theorem of algebra.
The theorem reveals that, in this case, up to four imaginary roots exist. Combining this fact with Descartes’s rule of signs gives you several possibilities:
One real positive root and one real negative root means that two roots aren’t real.
Three real positive roots and one real negative root means that all roots are real.
List the possible rational roots, using the rational root theorem.
The possible rational roots include
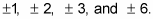
Determine the rational roots (if any), using synthetic division.
Utilizing the rules of synthetic division, you find that x = 1 is a root and that x = –3 is another root. These roots are the only real ones.
Use the quadratic formula to solve the depressed polynomial.
Having found all the real roots of the polynomial, divide the original polynomial by x-1 and the resulting polynomial by x+3 to obtain the depressed polynomial x2 – x + 2. Because this expression is quadratic, you can use the quadratic formula to solve for the last two roots. In this case, you get
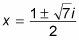
Graph the results.
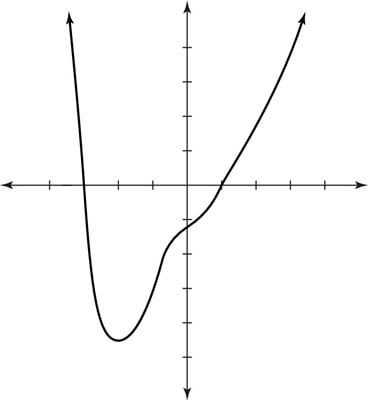 Graphing the polynomial g(x) = x4 + x3 – 3x2 + 7x – 6.
Graphing the polynomial g(x) = x4 + x3 – 3x2 + 7x – 6.The leading coefficient test reveals that the graph points up in both directions. The intervals include the following:
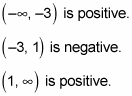
The preceding figure shows the graph of this function.

