Basic Math & Pre-Algebra All-in-One For Dummies (+ Chapter Quizzes Online)
Explore Book Buy On AmazonCompleting the square comes in handy when you’re asked to solve an unfactorable quadratic equation and when you need to graph conic sections (circles, ellipses, parabolas, and hyperbolas).
You should only find the roots of a quadratic using this technique when you’re specifically asked to do so, because factoring a quadratic and using the quadratic formula work just as well (if not better). Those methods are less complicated than completing the square (a pain in the you-know-where!).
For example, if your instructor calls for you to solve the equation 2x2 – 4x + 5 = 0, you can do so by completing the square:
Divide every term by the leading coefficient so that a = 1.
If the equation already has a plain x2 term, you can skip to Step 2.
Be prepared to deal with fractions in this step. Dividing each term by 2, the equation now becomes
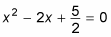
Subtract the constant term from both sides of the equation to get only terms with the variable on the left side of the equation.
You can subtract 5/2 from both sides to get
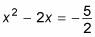
Now to complete the square: Divide the linear coefficient by 2 and write it below the problem for later, square this answer, and then add that value to both sides so that both sides remain equal.
Divide –2 by 2 to get –1. Square this answer to get 1, and add it to both sides:
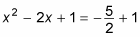
Simplify the equation.
The equation becomes
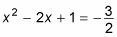
Factor the newly created quadratic equation.
The new equation should be a perfect-square trinomial.
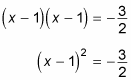
Get rid of the square exponent by taking the square root of both sides.
Remember that the positive and negative roots could both be squared to get the answer! This step gives you
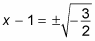
Simplify any square roots if possible.
The example equation doesn’t simplify, but the fraction is imaginary and the denominator needs to be rationalized. Do the work to get
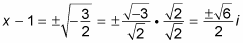
Solve for the variable by isolating it.
You add 1 to both sides to get
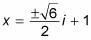
Note: You may be asked to express your answer as one fraction; in this case, find the common denominator and add to get