Exponential and Logarithmic Functions Used in Pre-Calculus

Exponential and logarithmic functions go together. You wouldn’t think so at first glance, because exponential functions can look like f(x) = 2e^3x, and logarithmic (log) functions can look like f(x) = ln(x² – 3). What joins them together is that exponential functions and log functions are inverses of each other.

Exponential and logarithmic functions can have bases that are any positive number except the number 1. The special cases are those with base 10 (common logarithms) and base e (natural logarithms), which go along with their exponential counterparts.

The whole point of these functions is to tell you how large something is when you use a particular exponent or how big of an exponent you need in order to create a particular number. These functions are heavily used in the sciences and finance, so studying them here can pay off big time in later studies.

You’ll work with exponential and logarithmic functions in the following ways:

• Evaluating exponential and log functions using the function rule

• Simplifying expressions involving exponential and log functions

• Solving exponential equations using rules involving exponents

• Solving logarithmic equations using laws of logarithms

• Graphing exponential and logarithmic functions for a better view of their powers

• Applying exponential and logarithmic functions to real-life situations

Don’t let common mistakes trip you up. Here are some of the challenges you’ll face when working with exponential and logarithmic functions:

• Using the rules for exponents in various operations correctly

• Applying the laws of logarithms to denominators of fractions

• Remembering the order of operations when simplifying exponential and log expressions

• Checking for extraneous roots when solving logarithmic equations

Practice problems

1. Graph the exponential function: f(x) = –3^x

   Answer:

   

   Credit: Illustration by Thomson Digital

   You find the x-intercepts by solving for f(x) = 0. No values of x make the equation true, so there are no x-intercepts.

   You find the y-intercept by substituting 0 for x: f(0) = –3⁰ = –1

   So the y-intercept is (0, –1).

   There’s a horizontal asymptote at y = 0 because the limit as x approaches

   

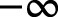
   is 0. The function is decreasing as x approaches

   

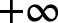
   because the values of the function are getting smaller and smaller, and the function approaches 0 as x approaches

   

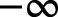
   because of the horizontal asymptote.

2. Solve the exponential equation for x:

   

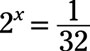
   Answer: x = ‒5

   First, rewrite the right side of the equation so that it has the same base as the left:

   

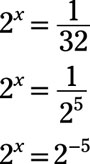
   The bases are now the same, so set the exponents on each side equal to each other: x = –5