The easy way always works, and you should use this method for most of your fraction subtracting needs. The quick trick is a great timesaver, so use it when you can. And as for the traditional way — well, your teacher and other math purists probably prefer you to use it this way.
Subtract fractions with the easy method
This way of subtracting fractions works in all cases, and it’s easy. Here’s the easy way to subtract fractions that have different denominators:-
Cross-multiply the two fractions and subtract the second number from the first to get the numerator of the answer.
For example, suppose you want to subtract 6/7 – 2/5. To get the numerator, cross-multiply the two fractions and then subtract the second number from the first number:
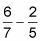
(6 5) – (2 7) = 30 – 14 = 16
After you cross-multiply, be sure to subtract in the correct order. (The first number is the numerator of the first fraction times the denominator of the second.)
-
Multiply the two denominators together to get the denominator of the answer.
7 5 = 35
-
Putting the numerator over the denominator gives you your answer.
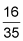
This example puts all the steps together:
With the problem set up like this, you just have to simplify the result:
In this case, you can reduce the fraction:
Subtract fractions with the quick trick method
The easy way works best when the numerators and denominators are small. When they’re larger, you may be able to take a shortcut.Before you subtract fractions with different denominators, check the denominators to see whether one is a multiple of the other. If it is, you can use the quick trick:
-
Increase the terms of the fraction with the smaller denominator so that it has the larger denominator.
For example, suppose you want to find 17/20 – 31/80. If you cross-multiply these fractions, your results are going to be much bigger than you want to work with. But fortunately, 80 is a multiple of 20, so you can use the quick way.
First, increase the terms of 17/20 so that the denominator is 80:
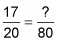
? = 80 ÷ 20 17 = 68
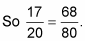
-
Rewrite the problem, substituting this increased version of the fraction, and subtract.
Here’s the problem as a subtraction of fractions with the same denominator, which is much easier to solve:
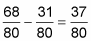
In this case, you don’t have to reduce to the lowest terms, although in other problems you may have to.
Subtract fractions with the traditional method
You should use the traditional way only as a last resort, when the numerator and denominator are too large to use the easy way and when you can’t use the quick trick.To use the traditional way to subtract fractions with two different denominators, follow these steps:
-
Find the least common multiple (LCM) of the two denominators.
For example, suppose you want to subtract 7/8 – 11/14. Here’s how to find the LCM of 8 and 14 using the prime factorization method:
8 = 2 2 2
14 = 2 7
In this example, the case where each prime factor appears most often is underlined: 2 appears three times, and 7 appears once. So the LCM of 8 and 14 is
2 2 2 7 = 56
-
Increase each fraction to higher terms so that the denominator of each equals the LCM.
The denominators of both should be 56:
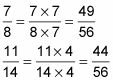
-
Substitute these two new fractions for the original ones and subtract.
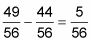
This time, you don’t need to reduce, because 5 is a prime number and 56 isn’t divisible by 5. In some cases, however, you have to reduce the answer to the lowest terms.

