When you cut a cake into two pieces and take one piece, you have 1/2 of the cake. And when you cut it into four pieces and take two, you have 2/4 of the cake. Finally, when you cut it into six pieces and take three, you have 3/6 of the cake. Notice that in all these cases, you get the same amount of cake.
This shows you that the fractions 1/2, 2/4, and 3/6 are equal; so are the fractions 10/20 and
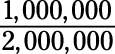
Most of the time, writing this fraction as 1/2 is preferred because the numerator and denominator are the smallest possible numbers. In other words, the fraction 1/2 is written in lowest terms. At the end of a problem, you often need to reduce a fraction, or write it in lowest terms. There are two ways to do this — the informal way and the formal way:
The informal way to reduce a fraction is to divide both the numerator and the denominator by the same number.
Advantage: The informal way is easy.
Disadvantage: It doesn’t always reduce the fraction to lowest terms (though you do get the fraction in lowest terms if you divide by the greatest common factor).
The formal way is to decompose both the numerator and the denominator into their prime factors and then cancel common factors.
Advantage: The formal way always reduces the fraction to lowest terms.
Disadvantage: It takes longer than the informal way.
Start every problem using the informal way. If the going gets rough and you’re still not sure whether your answer is reduced to lowest terms, switch over to the formal way.
Sometimes at the beginning of a fraction problem, you need to increase the terms of a fraction — that is, write that fraction using a greater numerator and denominator. To increase terms, multiply both the numerator and denominator by the same number.
Sample questions
Increase the terms of the fraction 4/5 to a new fraction whose denominator is 15:
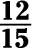
To start out, write the problem as follows:
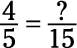
The question mark stands for the numerator of the new fraction, which you want to fill in. Now divide the larger denominator (15) by the smaller denominator (5).
15 / 5 = 3
Multiply this result by the numerator:
3 x 4 = 12
Finally, take this number and use it to replace the question mark:
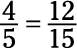
Reduce the fraction 18/42 to lowest terms.
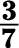
The numerator and denominator aren’t too large, so use the informal way: To start out, try to find a small number that the numerator and denominator are both divisible by. In this case, notice that the numerator and denominator are both divisible by 2, so divide both by 2:
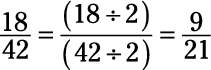
Next, notice that the numerator and denominator are both divisible by 3, so divide both by 3:

At this point, there’s no number (except for 1) that evenly divides both the numerator and denominator, so this is your answer.
Reduce the fraction 135/196 to lowest terms.
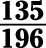
The numerator and denominator are both over 100, so use the formal way. First, decompose both the numerator and denominator down to their prime factors:
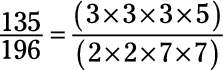
The numerator and denominator have no common factors, so the fraction is already in lowest terms.
Practice questions
Increase the terms of the fraction 2/3 so that the denominator is 18.
Increase the terms of 4/9, changing the denominator to 54.
Reduce the fraction 12/60 to lowest terms.
Reduce 45/75 to lowest terms.
Reduce the fraction 135/180 to lowest terms.
Reduce 108/217 to lowest terms.
Following are the answers to the practice questions:
-
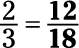
To start out, write the problem as follows:
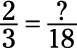
Divide the larger denominator (18) by the smaller denominator (3) and then multiply this result by the numerator (2):
6 x 2 = 12
Take this number and use it to replace the question mark; your answer is
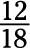
-
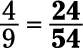
Write the problem as follows:
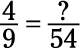
Divide the larger denominator (54) by the smaller denominator (9) and then multiply this result by the numerator (4):
6 x 4 = 24
Take this number and use it to replace the question mark; your answer is
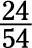
-
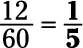
The numerator (12) and the denominator (60) are both even, so divide both by 2:
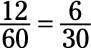
They’re still both even, so divide both by 2 again:
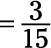
Now the numerator and denominator are both divisible by 3, so divide both by 3:
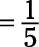
-
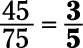
The numerator (45) and the denominator (75) are both divisible by 5, so divide both by 5:
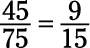
Now the numerator and denominator are both divisible by 3, so divide both by 3:
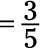
-
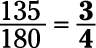
The numerator (135) and the denominator (180) are both divisible by 5, so divide both by 5:
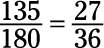
Now the numerator and denominator are both divisible by 3, so divide both by 3:
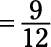
They’re still both divisible by 3, so divide both by 3 again:
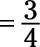
-
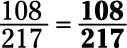
With a numerator and denominator this large, reduce using the formal way. First, decompose both the numerator and denominator down to their prime factors:
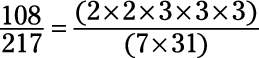
The numerator and denominator have no common factors, so the fraction is already in lowest terms.

