In the other type of experiment you try to estimate the probability of something even though controlling the conditions is impossible. For example, how likely is My Lovely Horse to win the 3.30 p.m. at Chepstow? What are the chances of it raining tomorrow?
Dice, cards and spinners
Setting up an experiment with dice, cards or spinners is easy but really boring. Here’s what you do:-
Decide how many trials you want to run.
How many times will you throw the die or spin the spinner?
-
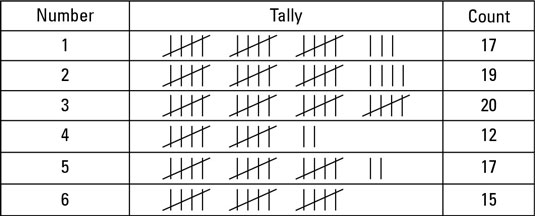
Set up a tally chart like the one shown.
-
If you’re using cards, shuffle them.
This helps you make the outcome as random as possible.
-
Run a trial!
Throw the die or pick a card or spin the spinner, as appropriate.
-
Record the result on your tally chart.
-
Go back to Step 3 over and over until you’ve completed all of the trials you decided you were going to run in Step 1.
How many times . . . ?
You can also work out how many times you expect an event with a given probability to occur if you run the experiment some number of times.Simply times the number of trials by the probability.
If you have the following exam question:
A spinner has a probability of 0.2 that it will land on red. If you spun the spinner 200 times, how often would you expect it to land on red?You simply work out 0.2 x 200 = 40 times.
Make sure your number is less than the number of trials – or else something has gone wrong.

