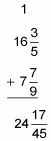How to Add Mixed Numbers

Whether mixed numbers have the same denominators or different denominators, adding them is a lot like adding whole numbers: you stack them up one on top of the other, draw a line, and add. For this reason, some students feel more comfortable adding mixed numbers than adding fractions.

Here’s how to add two mixed numbers:

1. Add the fractional parts and if necessary, change this sum to a mixed number and reduce it.

2. If the answer you found in Step 1 is an improper fraction, change it to a mixed number, write down the fractional part, and carry the whole number part to the whole number column.

3. Add the whole number parts (including any number carried).

Your answer may also need to be reduced to lowest terms. The examples that follow show you everything you need to know.

Add mixed numbers with the same denominators

As with any problem involving fractions, adding is always easier when the denominators are the same. For example, suppose you want to add 3 1/3 + 5 1/3. Doing mixed number problems is often easier if you place one number above the other:

As you can see, this arrangement is similar to how you add whole numbers, but it includes an extra column for fractions. Here’s how you add these two mixed numbers step by step:

1. Add the fractions.

   

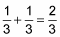
2. Switch improper fractions to mixed numbers; write down your answer.

   Because 2/3 is a proper fraction, you don’t have to change it.

3. Add the whole number parts.

   3 + 5 = 8

Here’s how your problem looks in column form:

This problem is about as simple as they get. In this case, all three steps are pretty easy. But sometimes, Step 2 requires more attention. For example, suppose you want to add 8 3/5 + 6 4/5. Here’s how you do it:

1. Add the fractions.

   

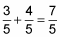
2. Switch improper fractions to mixed numbers, write down the fractional part, and carry over the whole number.

   Because the sum is an improper fraction, convert it to the mixed number 1 2/5. Write down 2/5 and carry the 1 over to the whole-number column.

3. Add the whole number parts, including any whole numbers you carried over when you switched to a mixed number.

   1 + 8 + 6 = 15

Here’s how the solved problem looks in column form. (Be sure to line up the whole numbers in one column and the fractions in another.)

As with any other problems involving fractions, sometimes you need to reduce at the end of Step 1.

Add mixed numbers with different denominators

The most difficult type of mixed number addition is when the denominators of the fractions are different. This difference doesn’t change Steps 2 or 3, but it does make Step 1 tougher.

For example, suppose you want to add 16 3/5 and 7 7/9.

1. Add the fractions.

   Add 3/5 and 7/9:

   

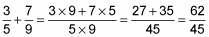
2. Switch improper fractions to mixed numbers, write down the fractional part, and carry over the whole number.

   This fraction is improper, so change it to the mixed number 1 17/45. Fortunately, the fractional part of this mixed number isn’t reducible.

   Write down the 17/45 and carry over the 1 to the whole-number column.

3. Add the whole numbers.

   1 + 16 + 7 = 24

Here’s how the completed problem looks: