Each of the sets of numbers listed here serves a different purpose, some familiar (such as accounting and carpentry), some scientific (such as electronics and physics), and a few purely mathematical.
Counting on counting (or natural) numbers
The counting numbers — also called the natural numbers — are probably the first numbers you ever encountered. They start with 1 and go up from there:
{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...}
The three dots (or ellipsis) at the end tell you that the sequence of numbers goes on forever — in other words, it's infinite.
If you place 0 in the set of counting numbers, you get the set of whole numbers.
Identifying integers
The set of integers includes the counting numbers, the negative counting numbers, and 0:
{..., –6, –5, –4, –3, –2, –1, 0, 1, 2, 3, 4, 5, 6, ...}
Knowing the rationale behind rational numbers
The rational numbers include the integers and all the fractions between the integers. Listed below is the set of rational numbers from –1 to 1 whose denominators (bottom numbers) are positive numbers less than 5:
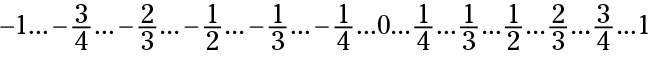
The ellipses tell you that between any pair of rational numbers is an infinite number of other rational numbers — a quality called the infinite density of rational numbers.
Rational numbers are commonly used for measurement in which precision is important.
Making sense of irrational numbers
In a sense, the irrational numbers are a sort of catchall; every number on the number line that isn't rational is irrational.
By definition, no irrational number can be represented as a fraction, nor can an irrational number be represented as either a terminating decimal or a repeating decimal. Instead, an irrational number can be approximated only as a nonterminating, nonrepeating decimal: the string of numbers after the decimal point goes on forever without creating a pattern.
The most famous example of an irrational number is pi, which represents the circumference of a circle with a diameter of 1 unit.
Irrational numbers fill out the spaces in the real number line. (The real number line is just the number line you're used to, but it's continuous; it has no gaps, so every point is paired with a number.) These numbers are used in many cases you need not just a high level of precision, as with the rational numbers, but the exact value of a number that you can't represent as a fraction.
Irrational numbers come in two varieties: algebraic numbers and transcendental numbers.
Absorbing algebraic numbers
To understand algebraic numbers, you need a little information about polynomial equations. A polynomial equation is an algebraic equation that meets the following conditions:
Its operations are limited to addition, subtraction, and multiplication. In other words, you don't have to divide by a variable.
Its variables are raised only to positive, whole-number exponents.
Here are some polynomial equations:
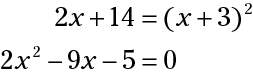
Moving through transcendental numbers
A transcendental number, in contrast to an algebraic number, is never the solution of a polynomial equation. Like the irrational numbers, transcendental numbers are a sort of catchall: Every number on the number line that isn't algebraic is transcendental.
The best-known transcendental number is pi, whose approximate value is 3.1415926535 . . .. Its uses begin in geometry but extend to virtually all areas of mathematics.
Getting grounded in real numbers
The set of real numbers is the set of all rational and irrational numbers. The real numbers comprise every point on the number line.
Trying to imagine imaginary numbers
An imaginary number is any real number multiplied by
To understand what's so strange about imaginary numbers, it helps to know a bit about square roots. The square root of a number is any value that, when multiplied by itself, gives you that number. For example, the square root of 9 is 3 because 3 x 3 = 9. And the square root of 9 is also –3 because –3 x –3 = 9.
The problem with finding
is that it isn't on the real number line. To be on the real number line, a number must be positive, negative, or 0. But when you multiply any positive number by itself, you get a positive number. And when you multiply any negative number by itself, you also get a positive number. Finally, when you multiply 0 by itself, you get 0.
Mathematicians designated
with the symbol i. Because it didn't fit onto the real number line, i got its own number line, which looks a lot like the real number line. The figure shows some numbers that form the imaginary number line.
Even though these numbers are called imaginary, mathematicians today consider them no less real than the real numbers. And the scientific application of imaginary numbers to electronics and physics has verified that these numbers are more than just figments of someone's imagination.
Grasping the complexity of complex numbers
A complex number is any real number plus or minus an imaginary number. Consider some examples:
1 + i 5 – 2i –100 + 10i
You can turn any real number into a complex number by just adding 0i (which equals 0):
3 = 3 + 0i –12 = –12 + 0i 3.14 = 3.14 + 0i
These examples show you that the real numbers are just a part of the larger set of complex numbers.
Going beyond the infinite with transfinite numbers
The transfinite numbers are a set of numbers representing different levels of infinity. Consider this for a moment: The counting numbers (1, 2, 3, . . .) go on forever, so they're infinite. But there are more real numbers than counting numbers.
In fact, the real numbers are infinitely more infinite than the counting numbers. Mathematician Georg Cantor proved this fact. He also proved that, for every level of infinity, you can find another level that's even higher. He called these ever-increasing levels of infinity transfinite, because they transcend, or go beyond, what you think of as infinite.
The lowest transfinite number is aleph null, which equals the number of elements in the set of counting numbers ({1, 2, 3, 4, 5,…}). The next transfinite number is aleph one, which equals the number of elements in the set of real numbers. This is a higher order of infinity than infinity.

