Numbers seem to have personalities all their own. For example, even numbers are go-along numbers that break in half so you can carry them more conveniently. Odd numbers are more stubborn and don't break apart so easily. Powers of ten are big friendly numbers that are easy to add and multiply, whereas most other numbers are prickly and require special attention.
Square numbers
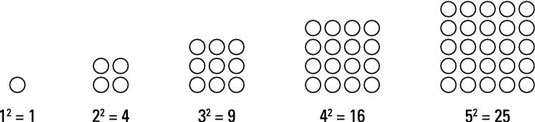
When you multiply any number by itself, the result is a square number. For example,
12 = 1 x 1 = 1
22 = 2 x 2 = 4
32 = 3 x 3 = 9
42 = 4 x 4 = 16
52 = 5 x 5 = 25
Therefore, the sequence of square numbers begins as follows:
1, 4, 9, 16, 25, . . .
To see why they're called square numbers, look at the arrangement of coins in squares:
Triangular numbers
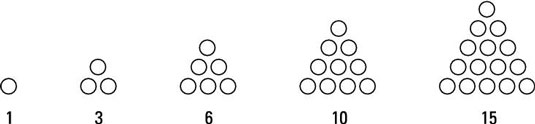
When you add up any sequence of consecutive positive numbers starting with 1, the result is a triangular number. For example,
1 = 1
1 + 2 = 3
1 + 2 + 3 = 6
1 + 2 + 3 + 4 = 10
1 + 2 + 3 + 4 + 5 = 15
So, the sequence of triangular numbers begins as follows:
1, 3, 6, 10, 15, . . .
Triangular numbers’ shapely name makes sense when you begin arranging coins in triangles.
Cubic numbers
If you're feeling that the square and triangular numbers are too flat, add a dimension and begin playing with the cubic numbers. You can generate a cubic number by multiplying any number by itself three times:
13 = 1 x 1 x 1 = 1
23 = 2 x 2 x 2 = 8
33 = 3 x 3 x 3 = 27
43 = 4 x 4 x 4 = 64
53 = 5 x 5 x 5 = 125
The sequence of cubic numbers begins as follows:
1, 8, 27, 64, 125, . . .
Cubic numbers live up to their name.

Factorial numbers
In math, the exclamation point (!) means factorial, so you read 1! as one factorial. You get a factorial number when you multiply any sequence of consecutive positive numbers, starting with the number itself and counting down to 1. For example,
1! = 1
2! = 2 x 1 = 2
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120
Thus, the sequence of factorial numbers begins as follows:
1, 2, 6, 24, 120, . . .
Factorial numbers are very useful in probability, which is the mathematics of how likely an event is to occur. With probability problems, you can figure out how likely you are to win the lottery or estimate your chances of guessing your friend's locker combination within the first few tries.
Powers of two
Multiplying the number 2 by itself repeatedly gives you the powers of two. For example,
21 = 2
22 = 2 x 2 = 4
23 = 2 x 2 x 2 = 8
24 = 2 x 2 x 2 x 2 = 16
25 = 2 x 2 x 2 x 2 x 2 = 32
Powers of two are the basis of binary numbers, which are important in computer applications. They're also useful for understanding Fermat numbers.
Perfect numbers
Any number that equals the sum of its own factors (excluding itself) is a perfect number. To see how this works, find all the factors of 6:
6: 1, 2, 3, 6
Now add up all these factors except 6:
1 + 2 + 3 = 6
These factors add up to the number you started with, so 6 is a perfect number.
Perfect numbers are few and far between. The sequence of perfect numbers begins with the following five numbers:
6; 28; 496; 8,128; 33,550,336; . . .
Amicable numbers
Amicable numbers are similar to perfect numbers, except they come in pairs. The sum of the factors of one number (excluding the number itself) is equal to the second number, and vice versa. For example, one amicable pair is 220 and 284. To see why, first find all the factors of each number:
220: 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, 110, 220
284: 1, 2, 4, 71, 142, 284
For each number, add up all the factors except the number itself:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
1 + 2 + 4 + 71 + 142 = 220
Notice that the factors of 220 add up to 284, and the factors of 284 add up to 220. That's what makes this pair of numbers amicable.
Prime numbers
Any number that has exactly two factors — 1 and itself — is called a prime number. For example, here are the first few prime numbers:
2, 3, 5, 7, 11, 13, 17, 19, . . .
Mersenne primes
Any number that's 1 less than a power of two is called a Mersenne number (named for French mathematician Marin Mersenne). Therefore, every Mersenne number is of the following form:
2n – 1 (where n is a nonnegative integer)
When a Mersenne number is also a prime number, it's called a Mersenne prime. For example,
22 – 1 = 4 – 1 = 3
23 – 1 = 8 – 1 = 7
25 – 1 = 32 – 1 = 31
27 – 1 = 128 – 1 = 127
213 – 1 = 8,192 – 1 = 8,191
Mersenne primes are of interest to mathematicians because they possess properties that ordinary prime numbers don't have. One of these properties is that they tend to be easier to find than other prime numbers. For this reason, the search for the largest known prime number is usually a search for a Mersenne prime.

