When a parallel-lines-with-transversal drawing contains more than three lines, identifying congruent and supplementary angles can be kind of challenging. The following figure shows you two parallel lines with two transversals.
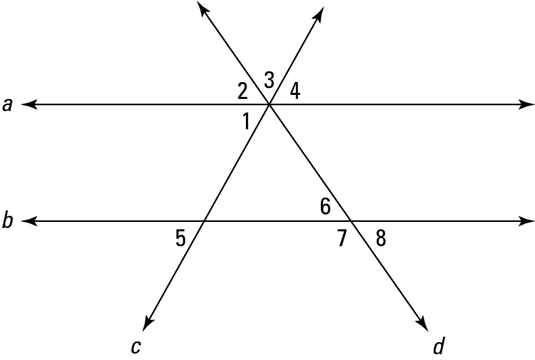
If you get a figure that has more than three lines and you want to use any of the transversal ideas, make sure you’re using only three of the lines at a time (two parallel lines and one transversal). If you aren’t using a set of three lines like this, the theorems just don’t work. With the above figure, you can use lines a, b, and c, or you can use lines a, b, and d, but you can’t use both transversals c and d at the same time. Thus, you can’t, for example, conclude anything about angle 1 and angle 6 because angle 1 is on transversal c and angle 6 is on transversal d.
The following list shows what you can say about several pairs of angles in the above figure, noting whether you can conclude that they’re congruent or supplementary. As you read through the list, remember the warning about using only two parallel lines and one transversal.
Angle pair 2 and 8 are congruent
Reason: Angle 2 and angle 8 are alternate exterior angles on transversal d
Angle pair 3 and 6 offer no conclusion
Reason: To make angle 3 you need to use transversals, c and d
Angle pair 4 and 5 are congruent
Reason: Angle 4 and angle 5 are alternate exterior angles on c
Angle pair 4 and 6 offer no conclusion
Reason: Angle 4 is on transversal c; angle 6 is on transversal d
Angle pair 2 and 7 is supplementary
Reason: Angle 2 and angle 7 are same-side exterior angles on d
Angle pair 1 and 8 offer no conclusion
Reason: Angle 1 is on transversal c; angle 8 is on transversal d
Angle pair 4 and 8 offer no conclusion
Reason: Angle 4 is on transversal c; angle 8 is on transversal d
If you get a figure with more than one transversal or more than one set of parallel lines, you may want to do the following: Trace the figure from your book to a sheet of paper and then highlight one pair of parallel lines and one transversal. (Or you can just trace the three lines you want to work with.) Then you can use the transversal ideas on the highlighted lines. After that, you can highlight a different group of three lines and work with those.
Of course, instead of tracing and highlighting, you can just make sure that the two angles you’re analyzing use only three lines (one ray of each angle should be part of the single transversal you’re using, and the other ray of each angle should be part of one of the two parallel lines you’re using).

