The Multiplication and division theorems are based on very simple ideas, but they do trip people up from time to time, so pay careful attention to how these theorems are used in the example proofs.
Like Multiples: If two segments (or angles) are congruent, then their like multiples are congruent. For example, if you have two congruent angles, then three times one will equal three times the other.
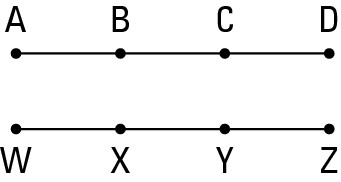
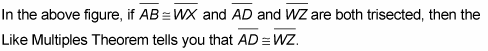
Like Divisions: If two segments (or angles) are congruent, then their like divisions are congruent. If you have, say, two congruent segments, then 1/4 of one equals 1/4 of the other, or 1/10 of one equals 1/10 of the other, and so on.
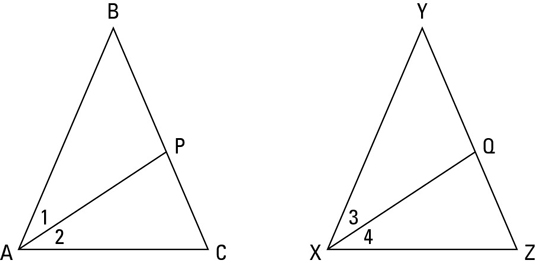
Look at the above figure.
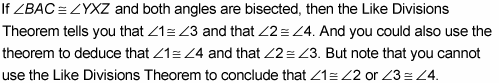
Those congruencies follow from the definition of bisect.
People sometimes get the Like Multiples and Like Divisions Theorems mixed up. Here’s a tip that’ll help you keep them straight: In a proof, you use the Like Multiples Theorem when you use congruent small segments (or angles) to conclude that two big segments (or angles) are congruent. You use the Like Divisions Theorem when you use congruent big things to conclude that two small things are congruent. In short, Like Multiples takes you from small to big; Like Divisions takes you from big to small.
When you look at the givens in a proof and you see one of the terms midpoint, bisect, or trisect mentioned twice, then you’ll probably use either the Like Multiples Theorem or the Like Divisions Theorem. But if the term is used only once, you’ll likely use the definition of that term instead.
You see how to use the Like Multiples Theorem in the next proof.

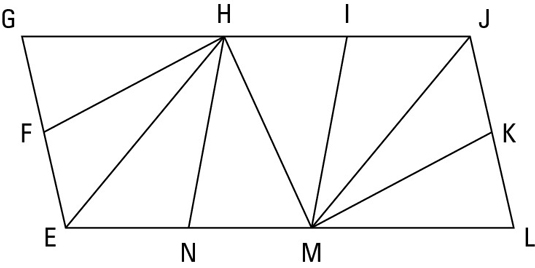
Game plan: Here’s how your thought process for this proof might go: Ask yourself how you can use the givens. In this proof, can you see what you can deduce from the two pairs of congruent angles in the given? If not, make up arbitrary measures for the angles.
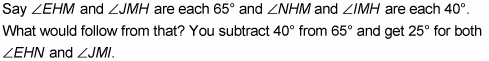
Then, when you see trisect mentioned twice in the other givens, that should ring a bell and make you think Like Multiples or Like Divisions.
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: Given.
Statement 3:
Reason for statement 3: If two congruent angles are subtracted from two other congruent angles, then the differences are congruent.
Statement 4:
Reason for statement 4: Given.
Statement 5:
Reason for statement 5: Given.
Statement 6:
Reason for statement 6: If two angles are congruent (angles EHN and JMI), then their like multiples are congruent (three times one equals three times the other).
Now for a proof that uses Like Divisions:


Here’s a possible game plan: What can you do with the first given? If you can’t figure that out right away, make up lengths for line segments ND, EL, and DE. Say that line segments ND and EL are both 12 and that line segment DE is 6. That would make both line segments NE and DL 18 units long. Then, because both of these segments are bisected by their midpoints, line segments NO and AL must both be 9. That’s a wrap.
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: If a segment is added to two congruent segments, then the sums are congruent.
Statement 3:

Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If two segments are congruent (line segments NE and DL), then their like divisions are congruent (half of one equals half of the other).
The Like Divisions Theorem is particularly easy to get confused with the definitions of midpoint, bisect, and trisect, so remember this: Use the definition of midpoint, bisect, or trisect when you want to show that parts of one bisected or trisected segment or angle are equal to each other. Use the Like Divisions Theorem when two objects are bisected or trisected (like line segments NE and DL in the preceding proof) and you want to show that a part of one (line segment NO) is equal to a part of the other (line segment AL).

