The SAS (Side-Angle-Side) postulate states that if two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. (The included angle is the angle formed by the two sides.) The following figure illustrates this method.
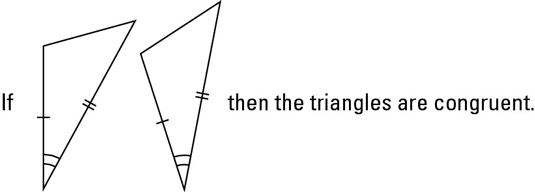
Check out the SAS postulate in action:
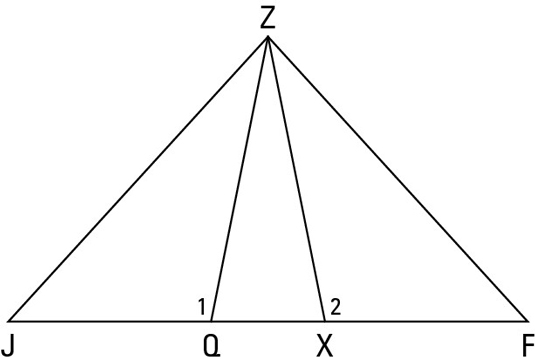
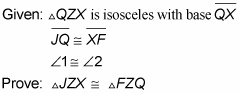
When overlapping triangles muddy your understanding of a proof diagram, try redrawing the diagram with the triangles separated. Doing so can give you a clearer idea of how the triangles’ sides and angles relate to each other. Focusing on your new diagram may make it easier to figure out what you need to do to prove the triangles congruent. However, you still need to use the original diagram to understand some parts of the proof, so use the second diagram as a sort of aid to get a better handle on the original diagram.
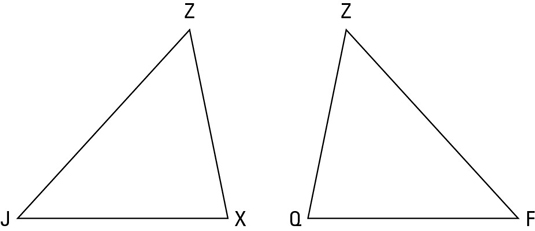
The above figure shows you what this proof diagram looks like with the triangles separated.
Looking at the figure, you can easily see that the triangles are congruent (they’re mirror images of each other).
So using both diagrams, here’s a possible game plan:
-
Determine which congruent triangle postulate is likely to be the ticket for proving the triangles congruent. You know you have to prove the triangles congruent, and one of the givens is about angles, so SAS looks like a better candidate than SSS (Side-Side-Side) for the final reason of the proof. (You don’t have to figure this out now, but it’s not a bad idea to at least have a guess about the final reason.)
-
Look at the givens and think about what they tell you about the triangles.
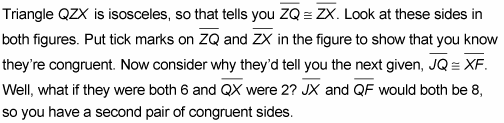
Put tick marks on the figure to show this congruence.
-
Find the pair of congruent angles. Look at the figure again. If you can show that angle X is congruent to angle Q, you’ll have SAS. Do you see where angle X and angle Q fit into the original diagram? Note that they’re the supplements of angle 1 and angle 2. That does it. Angles 1 and 2 are congruent, so their supplements are congruent as well. (If you fill in numbers, you can see that if angle 1 and angle 2 are both 100°, angle Q and angle X would both be 80°.)
Here’s the formal proof:
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: Definition of isosceles triangle.
Statement 3:
Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If a segment is added to two congruent segments, then the sums are congruent.
Statement 5:
Reason for statement 5: Given.
Statement 6:
Reason for statement 6: If two angles are supplementary to two other congruent angles, then they’re congruent.
Statement 7:
Reason for statement 7: SAS (using lines 2, 6, and 4)

