There are four subtraction theorems you can use in geometry proofs: two are for segments and two are for angles. Each of these corresponds to one of the addition theorems.
Here are the subtraction theorems for three segments and three angles (abbreviated as segment subtraction, angle subtraction, or just subtraction):
Segment subtraction (three total segments): If a segment is subtracted from two congruent segments, then the differences are congruent.
Angle subtraction (three total angles): If an angle is subtracted from two congruent angles, then the differences are congruent.
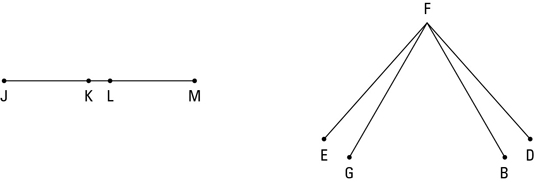
Check out the above figure, which provides the visual aids for these two theorems.

Last but not least, here are the subtraction theorems for four segments and for four angles (abbreviated just like the subtraction theorems for three things):
Segment subtraction (four total segments): If two congruent segments are subtracted from two other congruent segments, then the differences are congruent.
Angle subtraction (four total angles): If two congruent angles are subtracted from two other congruent angles, then the differences are congruent.
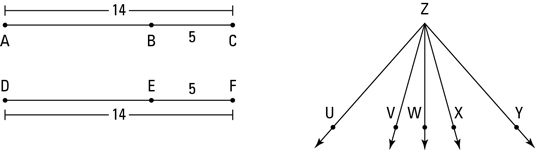
The above figure illustrates these two theorems.

Before reading the formal solution of the next proof, try to think through your own game plan or commonsense argument about why the prove statement has to be true.

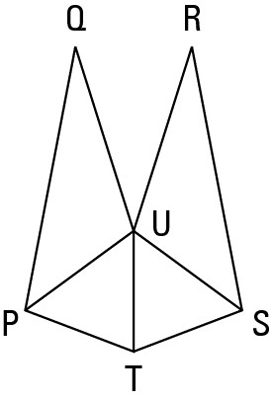
Statement 1:
Reason for statement 1: Given.
Statement 2:
Reason for statement 2: If an angle (angle QUR) is subtracted from two congruent angles (angles PUR and SUQ), then the differences are congruent.
Statement 3:
Reason for statement 3: Given.
Statement 4:
Reason for statement 4: If a ray bisects an angle, then it divides it into two congruent angles (definition of bisect).
Statement 5:
Reason for statement 5: If two congruent angles (the angles from statement 2) are added to two other congruent angles (the ones from statement 4), then the sums are congruent.

