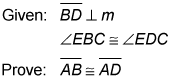Line-Plane perpendicularity definition: Saying that a line is perpendicular to a plane means that the line is perpendicular to every line in the plane that passes through its foot. (A foot is the point where a line intersects a plane.)
Line-Plane perpendicularity theorem: If a line is perpendicular to two different lines that lie in a plane and pass through its foot, then it's perpendicular to the plane.
In two-column proofs, you use the preceding definition and theorem for different reasons:- Use the definition when you already know that a line is perpendicular to a plane and you want to show that this line is perpendicular to a line that lies in the plane. In short:
- Use the theorem when you already know that a line is perpendicular to two lines in a plane and you want to show that the line is perpendicular to the plane itself. In short,
Note that this is roughly the reverse of the process in the definition.
Make sure you understand that a line must be perpendicular to two different lines in a plane before you can conclude that it's perpendicular to the plane. (The two lines in the plane will always intersect at the foot of the line that's perpendicular to the plane.) Perpendicularity to one line in a plane isn't enough.Here's why: Imagine you have a big capital letter L made out of, say, plastic, and you're holding it on a table so it's pointing straight up. When it's pointing up, the vertical piece of the L is perpendicular to the tabletop. Now start to tip the L a bit (keeping its base on the table), so the top of the L is now on a slant. The top piece of the L is obviously still perpendicular to the bottom piece (which is a line that's on the plane of the table), but the top piece of the L is no longer perpendicular to the table. Thus, a line sticking out of a plane can make a right angle with a line in the plane and yet not be perpendicular to the plane.
Okay, now it's time to apply all of this theory to a couple of problems:
Here's the diagram.
Now here's the proof:
Note: There are two other equally good ways to prove
which you see in statement 7. Both use the reflexive property for line EC, and then one method finishes, like here, with AAS; the other finishes with HLR. All three methods take the same number of steps. The method shown here is to reinforce the importance of the if-angles-then-sides theorem (reason 6).
The next example proof uses both the definition of and the theorem about line-plane perpendicularity.
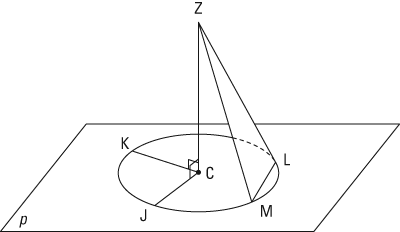
Here's the diagram.
Here's the formal proof: