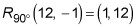When you transform geometric shapes, you may be changing their size, location, appearance, or all three. The following practice questions ask you to perform transformations that include reflection, rotation, translation, and dilation.
Practice questions
In a composition of transformations, two or more transformations are combined to form a new transformation. Find P, the image of P (5, 1) after a composition of transformations.
Answers and explanations
(1, 5)
When doing the composition of transformations, you perform the transformation closest to the point first. Therefore, you perform the transformations from right to left.
In this question, you rotate Point P 90 degrees counterclockwise first. Rotating 90 degrees counterclockwise about the origin is the same as reflecting over the line y = x and then reflecting over the y-axis. This means that the point (x, y) becomes the point (–y, x):
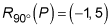
After completing the rotation, you reflect the point over the y-axis. Reflecting over the y-axis negates the x coordinate:
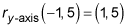
(1, 12)
First dilate Point P by a scale factor of 2. A dilation by a scale factor of 2 multiplies the x and y coordinates by 2:
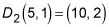
Next, you perform the translation. T2,–3 follows the rule (x + 2, y – 3):
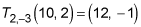
Last, rotate the point 90 degrees counterclockwise. Rotating 90 degrees counterclockwise about the origin is the same as reflecting over the line y = x and then reflecting over the y-axis. This means that the point (x, y) becomes the point (–y, x):