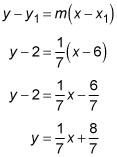In geometry, the Euler line is a serious multi-tasker: it contains the centroid, circumcenter, and orthocenter of a triangle. If you know any two of these points, you can determine the Euler line.
The following practice questions ask you, first, to use the equation for the Euler line to find the y-coordinate for the circumcenter of a triangle, and second, to find the equation for the Euler line given the triangle's centroid and orthocenter.
Practice questions
The equation for the Euler line of a triangle is
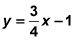
If the x coordinate of the circumcenter is 5, what is the y coordinate for the circumcenter?
The centroid of a triangle is (6, 2), and the orthocenter of the triangle is
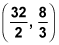
What is the equation of the Euler line for this triangle?
Answers and explanations
2.75
The circumcenter is on the Euler line. Find the y value by plugging x into the equation of the Euler line:
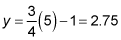
-
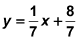
The Euler line is the line that contains the centroid, circumcenter, and orthocenter of a triangle. To find the equation of the line, you first need to determine the slope of the line that contains the two given points:
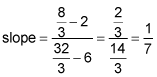
Then use the point-slope formula to find the equation of the line: