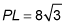In geometry, special right triangles are great to work with because the ratio of their sides will always be the same, making calculations easier. The two special triangles you need to know are the isosceles (or 45-45-90) and 30-60-90 right triangles.
You can use your knowledge of special right triangles to answer the following questions.
Practice questions
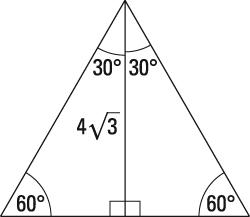
The length of the altitude of an equilateral triangle is
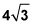
Find the length of a side of the triangle.
In isosceles right
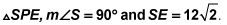
Rectangle PLCE,
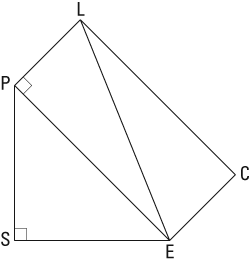
with diagonal
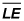
drawn forms a 30-degree angle at

Find the length of
Answers and explanations
8
An equilateral triangle is a triangle with three congruent sides and three congruent angles. Each angle therefore measures 60 degrees. When you draw the altitude, it creates two
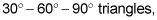
as in the following figure.
The pattern of the sides of a
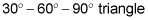
is as follows:

The altitude is the side opposite the 60-degree angle; therefore,
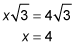
A side of the equilateral triangle is opposite the 90-degree angle, so it's equal to 2x; therefore, a side of the triangle equals
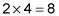
-
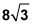
The pattern of the sides of an isosceles right triangle
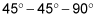
is as follows:

In this problem, the side opposite the 45-degree angle is
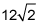
therefore,
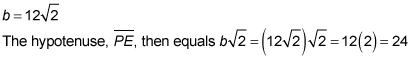
As shown in the figure,
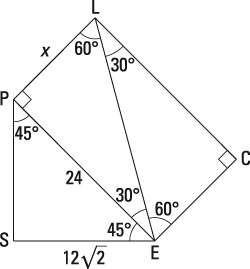
diagonal
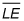
divides this rectangle into two
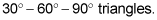
The pattern of the sides of a
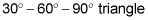
is as follows:

Line segment PE, measuring 24, is the side opposite the 60-degree angle, so it's equal to
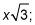
therefore,
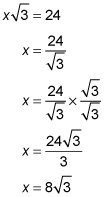
Line segment PL is the side opposite the 60-degree angle, so it equals x. Therefore,