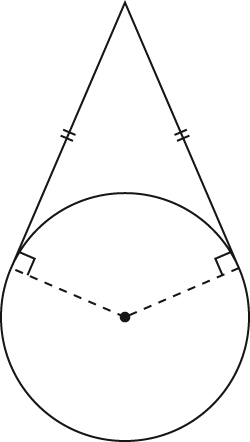
Dunce Cap Theorem: If two tangent segments are drawn to a circle from the same external point, then they're congruent. You can think of this as the dunce cap theorem because that's what the diagram for it looks like (although don't go searching for that name in a geometry book—you won't have much luck!).
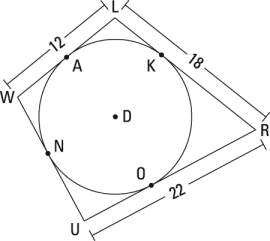
Try a problem.
Here's the proof diagram.
The first thing to notice about a walk-around problem is exactly what the dunce cap theorem says: Two tangent segments are congruent if they're drawn from the same point outside of the circle. So in this problem, you'd mark the following pairs of segments congruent:
(Are you starting to see why this is a walk-around solution?)
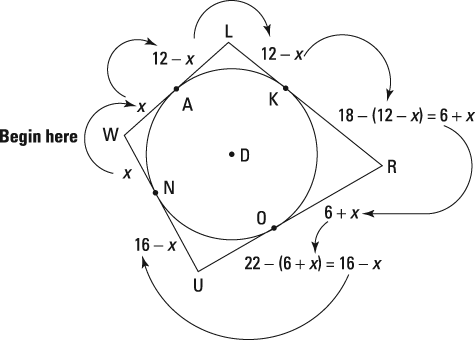
Okay, here's what you do. Set WN equal to x. Then, by the dunce cap theorem, WA is x as well. Next, because WL is 12 and WA is x, AL is 12 – x. A to L to K is another dunce cap, so LK is also 12 – x. LR is equal to 18, so KR is LR – LK or 18 – (12 – x); this simplifies to 6 + x. Continue walking around like this till you get back home to line NU, as you can see in the next figure.
Finally, UW equals WN + NU, or x + (16 – x), which equals 16. That's it.
One of the interesting things about walk-around problems is that when you have an even number of sides in the figure (as in this example), you get a solution without ever solving for x. In the example problem, x can take on any value from 0 to 12, inclusive. Varying x changes the size of the circle and the shape of the quadrilateral, but the lengths of the four sides (including the solution) remain unchanged. When, on the other hand, a walk-around problem involves an odd number of sides, there's a single solution for x and the diagram has a fixed shape. Pretty cool, eh?