To find the orthocenter of a triangle, you need to find the point where the three altitudes of the triangle intersect. In the following practice questions, you apply the point-slope and altitude formulas to do so.
Practice questions
Use your knowledge of the orthocenter of a triangle to solve the following problems.
The coordinates of
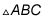
are A (0, 2), B (–2, 6), and C (4, 0). Find the coordinates of the orthocenter of this triangle.
The coordinates of
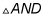
are A (0, 0), N (6, 0), and D (–2, 8). Find the coordinates ofthe orthocenter of this triangle.
Answers and explanations
(–8, –6)
The orthocenter of a triangle is the point where the three altitudes of the triangle intersect. An altitude of a triangle is perpendicular to the opposite side. Because perpendicular lines have negative reciprocal slopes, you need to know the slope of the opposite side. Here's the slope of
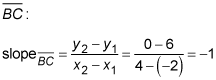
This means that the slope of the altitude to
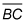
needs to be 1.
The point-slope formula of a line is y – y1 = m (x – x1), where m is the slope and (x1, y1) are the coordinates of a point on the line. To find the altitude formed when you connect Point A to
plug in m = –1 and the coordinates of Point A, (0, 2):
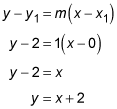
The slope of
is
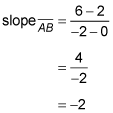
This means that the slope of the altitude to
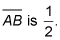
The altitude formed when you connect Point C, (4, 0), to
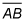
is
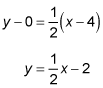
To find the orthocenter, you need to find where these two altitudes intersect. Set them equal and solve for x:
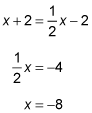
Now plug the x value into one of the altitude formulas and solve for y:
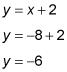
Therefore, the altitudes cross at (–8, –6).
(–2, –2)
The orthocenter of a triangle is the point where the three altitudes of the triangle intersect. An altitude of a triangle is perpendicular to the opposite side. Because perpendicular lines have negative reciprocal slopes, you need to know the slope of the opposite side. Here's the slope of
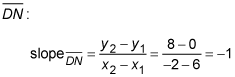
This means that the slope of the altitude to
needs to be 1.
The point-slope formula of a line is y – y1 = m (x – x1), where m is the slope and (x1, y1) are the coordinates of a point on the line. To find the altitude formed when you connect Point A to
plug in m = 1 and the coordinates of A, (0, 0):
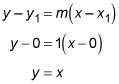
Now find the equation for the altitude to
The slope of
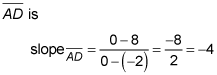
This means that the slope of the altitude to
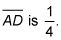
The altitude formed when you connect Point N, (6, 0), to
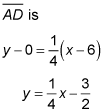
To find the orthocenter, you need to find where the two altitudes intersect. Set them equal and solve for x:
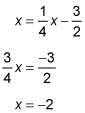
Now plug the x value into one of the altitude formulas and solve for y:
y = x
y = –2
Therefore, the altitudes cross at (–2, –2).

