Once you get to know the types of angles and how to measure and create your own, you'll have picked up valuable geometry skills that will help you prove even the most complex geometric puzzles.
To do both tasks, you use a protractor, a very useful tool to keep around (see Figure 1).
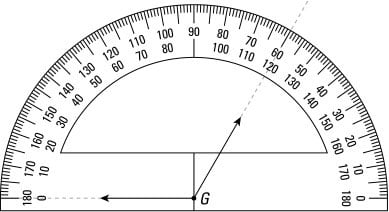 Figure 1: The handy-dandy protractor
Figure 1: The handy-dandy protractorWhen choosing a protractor, try to find one made of clear plastic. Figuring out the measure of an angle is easier because you can see the line for the angle through the protractor.
The breeds of angles
Several different angle breeds, or types, exist. You can figure out what breed of angle you have by its measure. The most common measure of an angle is in degrees. Here is a brief introduction to the four types of angles:- Right angle. With this angle, you can never go wrong. The right angle is one of the most easily recognizable angles. It's in the form of the letter L, and it makes a square corner (see Figure 2). It has a measure of 90 degrees.
 Figure 2: A right angle
Figure 2: A right angle- Straight angle. You know what? It's actually a straight line. Most people don't even think of this type as an angle, but it is. A straight angle is made up of opposite rays or line segments that have a common endpoint (see Figure 3). This angle has a measure of 180 degrees.
Right and straight angles are pretty easy to spot just by looking at them, but never jump to conclusions about the measure of an angle. Being cautious is best. If the info isn't written on the page, don't assume anything. Measure.
 Figure 3: A straight angle
Figure 3: A straight angle- Acute angle. It's the adorable angle.
- Actually, it's just a pinch. It's any angle that measures more than 0 degrees but less than 90 degrees. An acute angle falls somewhere between nonexistent and a right angle (see Figure 4).
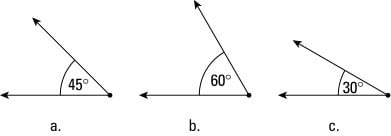 Figure 4: Acute angles, at 45° (Figure a), 60° (Figure b), and 30° (Figure c)
Figure 4: Acute angles, at 45° (Figure a), 60° (Figure b), and 30° (Figure c)- Obtuse angle. This type is just not as exciting as an acute angle. It's measure is somewhere between a right angle and a straight angle (see Figure 5). It is a hill you must climb, a mountain for you to summit. It has a measure of more than 90 degrees but less than 180 degrees.
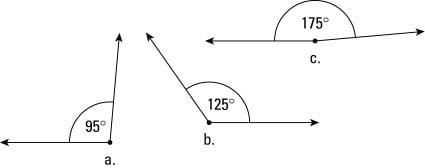 Figure 5: Obtuse angles, at 95° (Figure a), 125° (Figure b), and 175° (Figure c)
Figure 5: Obtuse angles, at 95° (Figure a), 125° (Figure b), and 175° (Figure c)Measuring angles
Angles are most commonly measured by degrees, but for those of you who are sticklers for accuracy, even smaller units of measure can be used: minutes and seconds. These kinds of minutes and seconds are like the ones on a clock — a minute is bigger than a second. So think of a degree like an hour, and you've got it down: One degree equals 60 minutes. One minute equals 60 seconds.Before measuring an angle, spec it out and estimate which type you think it is. Is it a right angle? A straight angle? Acute or obtuse? After you estimate it, then measure the angle. Follow these steps:
- Place the notch or center point of your protractor at the point where the sides of the angle meet (the vertex).
- Place the protractor so that one of the lines of the angle you want to measure reads zero (that's actually 0°). Using the zero line isn't necessary because you can measure an angle by getting the difference in the degree measures of one line to the other. It's easier, however, to measure the angle when one side of it is on the zero line. Having one line on the zero line allows you to read the measurement directly off the protractor without having to do more math. (But if you're up for the challenge, knock yourself out.)
- Read the number off the protractor where the second side of the angle meets the protractor.
- Make sure that your measure is close to your estimate. Doing so tells you whether you chose the proper scale. If you were expecting an acute angle measure but got a seriously obtuse measure, you need to rethink the scale you used. Try the other one.
- If the sides of your angle don't reach the scale of your protractor, extend them so that they do. Doing so increases the accuracy of your measure.
- Remember that the measure of an angle is always a positive number.
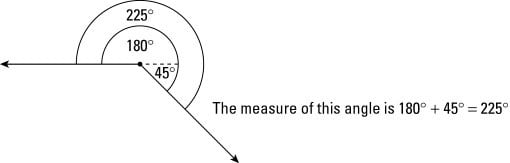 Figure 6: Reflex angles don't fit on the protractor's scale, so you need to do some math to measure them.
Figure 6: Reflex angles don't fit on the protractor's scale, so you need to do some math to measure them.
