CASTC is simply an acronym that stands for ‘Corresponding angles of similar triangles are congruent.’ You often use CASTC in a proof immediately after proving triangles similar (in precisely the same way that you use CPCTC after proving triangles congruent).
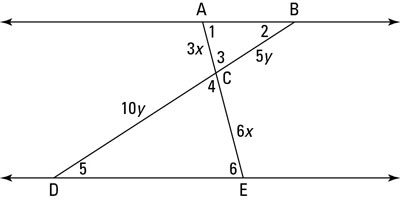
The following proof shows you how CASTC works:
Here’s how your game plan might go: When you see the two triangles in this proof diagram and you’re asked to prove that the lines are parallel, you should be thinking about proving the triangles similar. Then, using CASTC, you’ve got congruent angles that you can use with the parallel-line theorems to finish.
So here’s the solution. You’ve got the pair of congruent vertical angles, angle 3 and angle 4, so if you could show that the sides that make up those angles are proportional, the triangles would be similar by SAS~ (Side-Angle-Side). So check that the sides are proportional:

(Note that the similarity is written so that corresponding vertices pair up.)


