How to Solve Problems with the Altitude-0n-Hypotenuse Theorem

In a right triangle, the altitude that’s perpendicular to the hypotenuse has a special property: it creates two smaller right triangles that are both similar to the original right triangle.

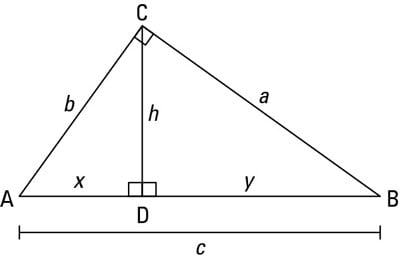
Altitude-on-Hypotenuse Theorem: If an altitude is drawn to the hypotenuse of a right triangle as shown in the above figure, then

Note that the two equations in the third part of the theorem are really just one idea, not two. It works exactly the same way on both sides of the big triangle:

Here’s a problem: use the figure below to answer the following questions.

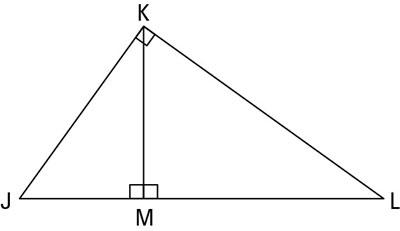
1. If JL = 17 and KL = 15, what are JK, JM, ML, and KM?

   Here’s how you do this one: JK is 8 because you have an 8-15-17 triangle (or you can get JK with the Pythagorean Theorem). Now you can find JM and ML using part three of the Altitude-on-Hypotenuse Theorem:

   

   (The ML solution is included just to show you another example of the theorem, but obviously, it would’ve been easier to get ML by just subtracting JM from JL.)

   Finally, use the second part of the theorem (or the Pythagorean Theorem, if you prefer) to get KM:

   

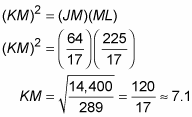
2. If ML = 16 and JK = 15, what’s JM?

   Set JM equal to x; then use part three of the theorem.

   

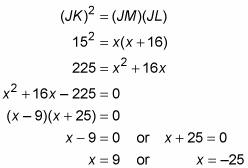
   You know that a length can’t be –25, so JM = 9. (If you have a hard time seeing how to factor this one, you can use the quadratic formula to get the values of x instead.)

When doing a problem involving an altitude-on-hypotenuse diagram, don’t assume that you must use the second or third part of the Altitude-on-Hypotenuse Theorem. Sometimes, the easiest way to solve the problem is with the Pythagorean Theorem. And at other times, you can use ordinary similar-triangle proportions to solve the problem.

The next problem illustrates this tip: Use the following figure to find h, the altitude of triangle ABC.

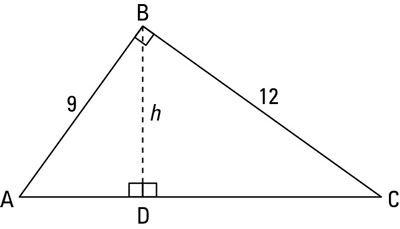
On your mark, get set, go. First get AC with the Pythagorean Theorem or by noticing that you have a triangle in the 3 : 4 : 5 family — namely a 9-12-15 triangle. So AC = 15. Then, though you could finish with the Altitude-on-Hypotenuse Theorem, but that approach is a bit complicated and would take some work. Instead, just use an ordinary similar-triangle proportion:

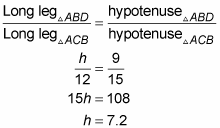
Finito.