The common-tangent problem is named for the single tangent segment that’s tangent to two circles. Your goal is to find the length of the tangent. These problems are a bit involved, but they should cause you little difficulty if you use the straightforward three-step solution method that follows.
The following example involves a common external tangent (where the tangent lies on the same side of both circles). You might also see a common-tangent problem that involves a common internal tangent (where the tangent lies between the circles). No worries: The solution technique is the same for both.

Here’s how to solve it:
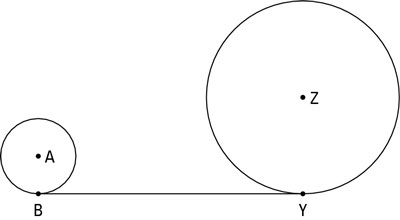
Draw the segment connecting the centers of the two circles and draw the two radii to the points of tangency (if these segments haven’t already been drawn for you).
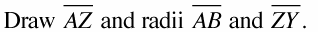
The following figure shows this step. Note that the given distance of 8 between the circles is the distance between the outsides of the circles along the segment that connects their centers.
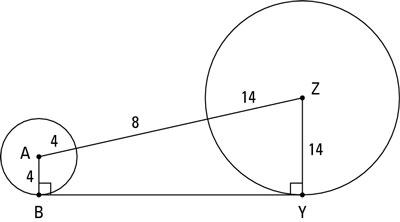
From the center of the smaller circle, draw a segment parallel to the common tangent till it hits the radius of the larger circle (or the extension of the radius in a common-internal-tangent problem).
You end up with a right triangle and a rectangle; one of the rectangle’s sides is the common tangent. The following figure illustrates this step.
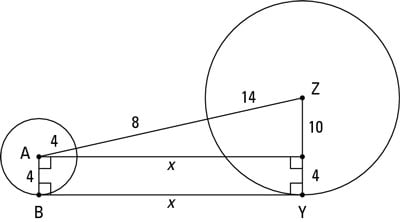
You now have a right triangle and a rectangle and can finish the problem with the Pythagorean Theorem and the simple fact that opposite sides of a rectangle are congruent.
The triangle’s hypotenuse is made up of the radius of circle A, the segment between the circles, and the radius of circle Z. Their lengths add up to 4 + 8 + 14 = 26. You can see that the width of the rectangle equals the radius of circle A, which is 4; because opposite sides of a rectangle are congruent, you can then tell that one of the triangle’s legs is the radius of circle Z minus 4, or 14 – 4 = 10. You now know two sides of the triangle, and if you find the third side, that’ll give you the length of the common tangent. You get the third side with the Pythagorean Theorem:
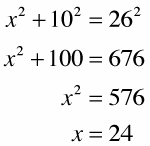
(Of course, if you recognize that the right triangle is in the 5 : 12 : 13 family, you can multiply 12 by 2 to get 24 instead of using the Pythagorean Theorem.)
Because opposite sides of a rectangle are congruent, BY is also 24, and you’re done.
Now look back at the last figure and note where the right angles are and how the right triangle and the rectangle are situated; then make sure you heed the following tip and warning.
Note the location of the hypotenuse. In a common-tangent problem, the segment connecting the centers of the circles is always the hypotenuse of a right triangle. The common tangent is always the side of a rectangle, not a hypotenuse.
In a common-tangent problem, the segment connecting the centers of the circles is never one side of a right angle. Don’t make this common mistake.

