There are three ways to prove that a quadrilateral is a rectangle. Note that the second and third methods require that you first show (or be given) that the quadrilateral in question is a parallelogram:
If all angles in a quadrilateral are right angles, then it’s a rectangle (reverse of the rectangle definition). (Actually, you only need to show that three angles are right angles — if they are, the fourth one is automatically a right angle as well.)
If the diagonals of a parallelogram are congruent, then it’s a rectangle (neither the reverse of the definition nor the converse of a property).
If a parallelogram contains a right angle, then it’s a rectangle (neither the reverse of the definition nor the converse of a property).
Tip: Do the following to visualize why this method works: Take an empty cereal box and push in the top flaps. If you then look into the empty box, the top of the box makes a rectangular shape, right? Now, start to crush the top of the box — you know, like you want to make it flat before putting it in the trash. As you start to crush the top of the box, you see a parallelogram shape. Now, after you’ve crushed it a bit, if you take this parallelogram and make one of the angles a right angle, the whole top has to become a rectangle again. You can’t make one of the angles a right angle without the other three also becoming right angles.
Before looking at any of these proof methods in action, here’s a useful little theorem that you need to do the upcoming proof.
Congruent supplementary angles are right angles: If two angles are both supplementary and congruent, then they’re right angles. This idea makes sense because 90° + 90° = 180°.
Okay, so here’s the proof:
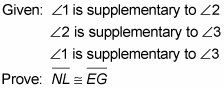
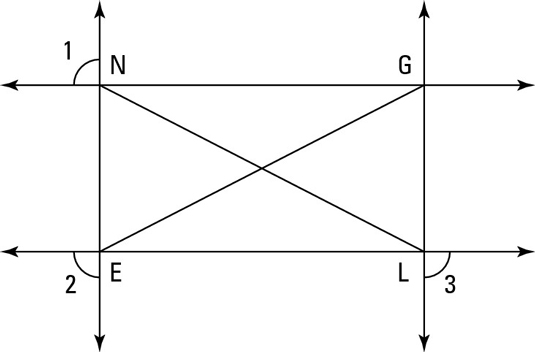
Statement 1:
Reason for statement 1: Given.
Statement 2:
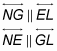
Reason for statement 2: If same-side exterior angles are supplementary, then lines are parallel.
Statement 3:
Reason for statement 3: If both pairs of opposite sides of a quadrilateral are parallel, then the quadrilateral is a parallelogram.
Statement 4:
Reason for statement 4: If two angles are supplementary to the same angle, then they’re congruent.
Statement 5:
Reason for statement 5: Given.
Statement 6:
Reason for statement 6: If two angles are both supplementary and congruent, then they’re right angles.
Statement 7:
Reason for statement 7: If lines form a right angle, then they’re perpendicular.
Statement 8:
Reason for statement 8: If lines are perpendicular, then they form right angles.
Statement 9:
Reason for statement 9: If a parallelogram contains a right angle, then it’s a rectangle.
Statement 10:
Reason for statement 10: The diagonals of a rectangle are congruent.

