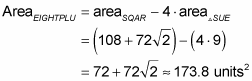For example, here’s how you’d find the area of EIGHTPLU in the figure below, given that it’s a regular octagon with sides of length 6.
The four corners (like triangle SUE in the figure) that you cut off the square to turn it into an octagon are 45°- 45°- 90° triangles (you can prove that to yourself if you feel like it). So all you have to do to get the area of the octagon is to calculate the area of the square and then subtract the four corner triangles. Piece o’ cake.
But first, here are two great tips for this and other problems.
-
For problems involving regular octagons, 45°- 45°- 90° triangles can come in handy. Add segments to the diagram to get one or more 45°- 45°- 90° triangles and some squares and rectangles to help you solve the problem.
-
Think outside the box. It’s easy to get into the habit of looking only inside a figure because that suffices for the vast majority of problems. But occasionally (like in this problem), you need to break out of that rut and look outside the perimeter of the figure.
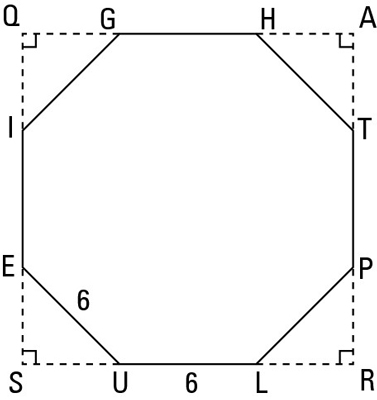

Not just calculate the area of the square and the area of a single corner triangle:
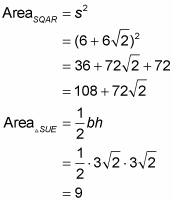
To finish, subtract the total area of the four corner triangles from the area of the square: