Although individual points have no features, when you group them, you can create several different types of points: collinear, non-collinear, coplanar, and non-coplanar. Each type merits an explanation:
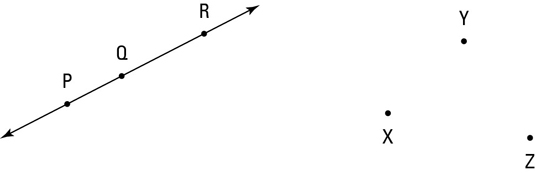
Collinear points: See the word line in collinear? Collinear points are points that lie on a line. Any two points are always collinear because you can always connect them with a straight line. Three or more points can be collinear, but they don’t have to be. The above figure shows collinear points P, Q, and R which all lie on a single line.
Non-collinear points: These points, like points X, Y, and Z in the above figure, don’t all lie on the same line.
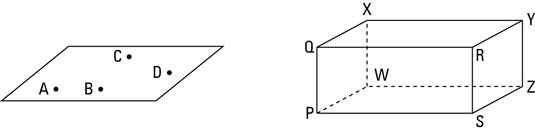
Coplanar points: A group of points that lie in the same plane are coplanar. Any two or three points are always coplanar. Four or more points might or might not be coplanar.
The left side of the above figure shows coplanar points A, B, C, and D. And in the box on the right, there are many sets of coplanar points. Points P, Q, X, and W, for example, are coplanar; the plane that contains them is the left side of the box. Each of the six faces of the box contains four coplanar points, but these are not the only groups of coplanar points. For example points Q, X, S, and Z are coplanar even though the plane that contains them isn’t shown; it slices the box in half diagonally.
Non-coplanar points: A group of points that don’t all lie in the same plane are non-coplanar.
In the above figure, points P, Q, X, and Y are non-coplanar. The top of the box contains Q, X, and Y, and the left side contains P, Q, and X, but no flat surface contains all four points.

