In geometry, you may be asked to formulate a proof with overlapping triangles. In order to prove parts of a triangle are congruent, you first need to prove that the triangles are congruent to each other.
The following example asks you to do just that.
Practice questions
Use the following figure to answer the questions regarding overlapping triangles.
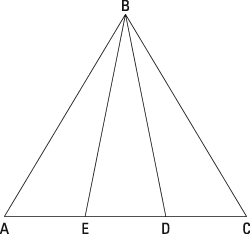
Given:
Prove:
The following questions ask you to fill in the blanks in the table.
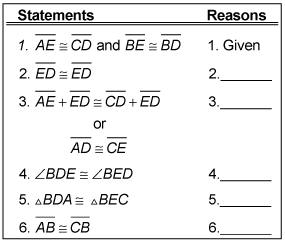
What is the reason for Statement 2?
What is the reason for Statement 3?
What is the reason for Statement 4?
What is the reason for Statement 5?
What is the reason for Statement 6?
Answers and explanations
Reflexive property
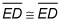
because a segment is congruent to itself.
Addition postulate
The addition postulate states that if two segments are congruent to two other segments, then the sums of the segments are also congruent to each other. Therefore,
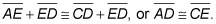
If two sides of a triangle are congruent, the angles opposite those sides are also congruent.
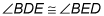
because they're the angles opposite the congruent sides

SAS
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent by SAS (side-angle-side). Therefore,
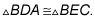
CPCTC
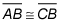
because corresponding parts of congruent triangles are congruent to each other.

