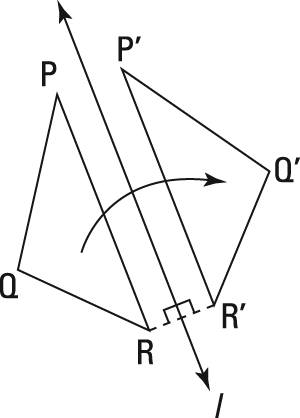
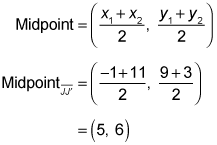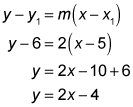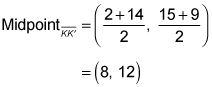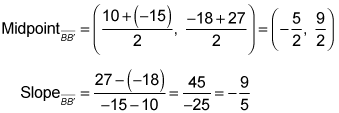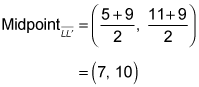This figure illustrates an important property of reflecting lines: If you form segment RR' by connecting pre-image point R with its image point R' (or P with P' or Q with Q'), the reflecting line, l, is the perpendicular bisector of segment RR'.
A reflecting line is a perpendicular bisector. When a figure is reflected, the reflecting line is the perpendicular bisector of all segments that connect pre-image points to their corresponding image points.
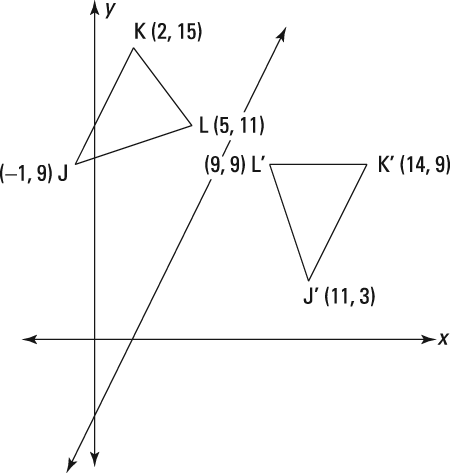
Here's a problem that uses this idea: In the following figure, triangle J'K'L' is the reflection of triangle JKL over a reflecting line. Find the equation of the reflecting line using points J and J'. Then confirm that this reflecting line sends K to K' and L to L'.The reflecting line is the perpendicular bisector of segments connecting pre-image points to their image points. Because the perpendicular bisector of a segment goes through the segment's midpoint, the first thing you need to do to find the equation of the reflecting line is to find the midpoint of line segment JJ':
Next, you need the slope of line segment JJ':
Now you can finish the first part of the problem by plugging the slope of 2 and the point (5, 6) into the point-slope form for the equation of a line:
That's the equation of the reflecting line, in slope-intercept form.
To confirm that this reflecting line sends K to K' and L to L', you have to show that this line is the perpendicular bisector of line segments KK' and LL'. To do that, you must show that the midpoints of line segments KK' and LL' lie on the line and that the slopes of line segments KK' and LL' are both –1/2 (the opposite reciprocal of the slope of the reflecting line, y = 2x – 4). First, here's the midpoint of line segment KK':
Plug these coordinates into the equation y = 2x – 4 to see whether they work. Because 12 = 2 (8) – 4, the midpoint of line segment KK' lies on the reflecting line. Now get the slope of line segment KK':
This is the desired slope, so everything's copasetic for K and K'. Now compute the midpoint of line segment LL':
Check that these coordinates work when you plug them into the equation of the reflecting line, y = 2x – 4. Because 10 = 2(7) – 4, the midpoint of line segment LL' is on the line. Finally, find the slope of line segment LL':
This checks. You're done.