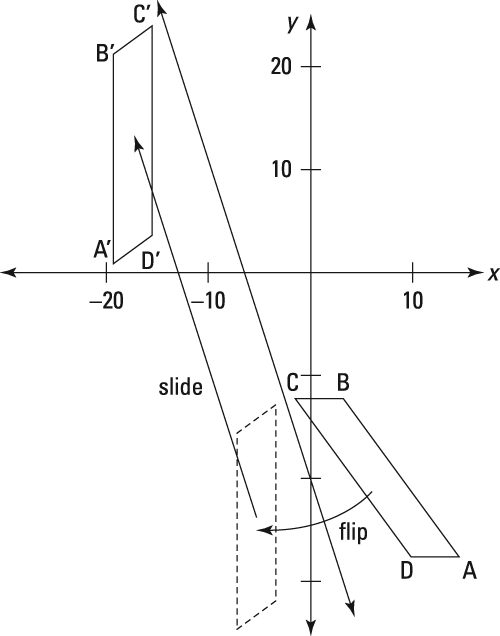
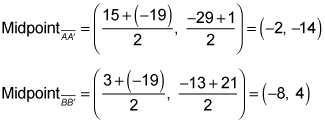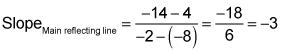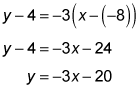The main reflecting line of a glide reflection: In a glide reflection, the midpoints of all segments that connect pre-image points with their image points lie on the main reflecting line.
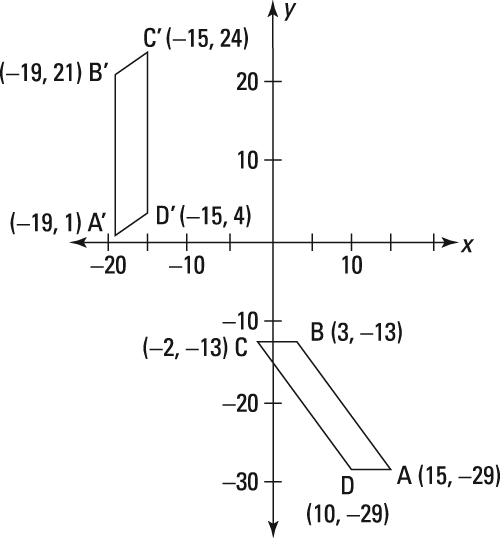
Ready for a glide reflection problem? This example will show you how to do the reflection first and then the translation, but you can do them in either order.The following figure shows a pre-image parallelogram ABCD and the image parallelogram A'B'C'D' that resulted from a glide reflection. You job is to find the main reflecting line.
The main reflecting line in a glide reflection contains the midpoints of all segments that join pre-image points with their image points (such as CC'). You need only two such midpoints to find the equation of the main reflecting line (because you need just two points to determine a line). The midpoints of AA' and BB' will do the trick:
Now simply find the equation of the line determined by these two points:
Use this slope and one of the midpoints in the point-slope form and simplify:
That's the main reflecting line. If you reflect parallelogram ABCD over this line, it'll then be in the same orientation as parallelogram A'B'C'D' (A to B to C to D will be in the clockwise direction), and ABCD will be perfectly vertical like A'B'C'D'. Then a simple translation in the direction of the main reflecting line will bring ABCD to A'B'C'D', as shown here.