Find the Locus of Points Equidistant from Two Points

If that sounds a little technical, don't worry—the following example will make everything clear!

To find the locus of all points equidistant from two given points, follow these steps:

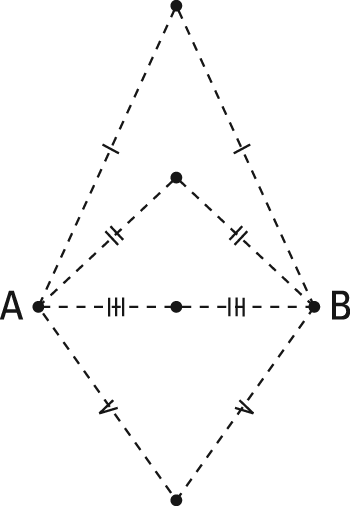
1. Identify a pattern. The figure shows the two given points, A and B, along with four new points that are each equidistant from the given points.
   

   Identifying points that work.

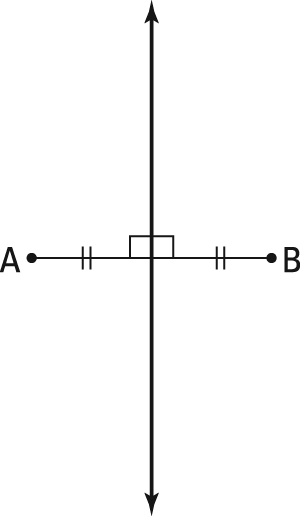
   Do you see the pattern? You got it—it's a vertical line that goes through the midpoint of the segment that connects the two given points. In other words, it's that segment's perpendicular bisector.

2. Look outside the pattern. You come up empty in Step 2. Check any point not on the perpendicular bisector of line AB, and you see that it's not equidistant from A and B. Thus, you have no points to add.
3. Look inside the pattern. Nothing noteworthy here, either. Every point on the perpendicular bisector of line AB is, in fact, equidistant from A and B. Thus, no points should be excluded. (Warning: Don't allow yourself to get a bit lazy and skip Steps 2 and 3!)
4. Draw the locus and describe it in words. This figure shows the locus, and the caption gives its description.

The locus of points equidistant from two given points is the perpendicular bisector of the segment that joins the two points.