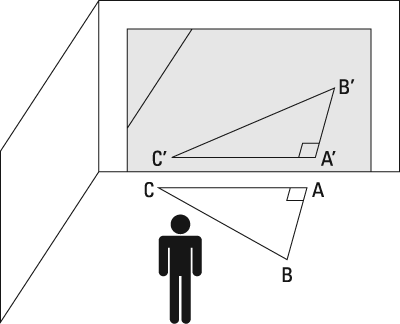
The figure shows someone in front of a mirror looking at the reflection of a triangle that's on the floor in front of the mirror. Note that the image of triangle ABC in the mirror is labeled with the same letters except a prime symbol is added to each letter
Most transformation diagrams are handled this way.
As you can see, the image of the triangle in the mirror is flipped over compared with the real triangle. Mirrors (and mathematically speaking, reflections) always produce this kind of flipping. Flipping a figure switches its orientation.
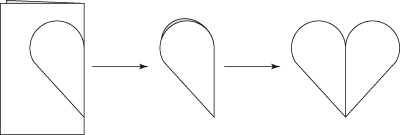
As you can see in the next figure, a reflection can also be thought of as a folding. On the left, you see a folded card with a half-heart shape drawn on it; in the center, you see the folded half-heart that's been cut out; and on the right, you see the heart unfolded. The left and right sides of the heart are obviously the same shape. Each side is the reflection of the other side. The crease or fold-line running down the center of the heart is called the reflecting line. (You probably didn't realize that when you were making valentines in first grade, you were dealing with mathematical isometries!)
Reflections are the building blocks of the other three isometries. You can produce the other isometries with a series of reflections:
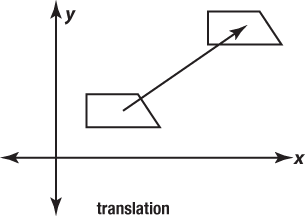
- Translations are the equivalent of two reflections.
- Rotations are the equivalent of two reflections.
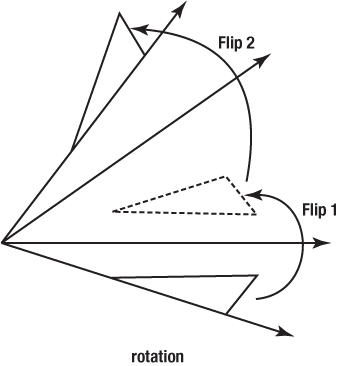
- Glide reflections are the equivalent of three reflections.