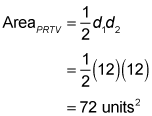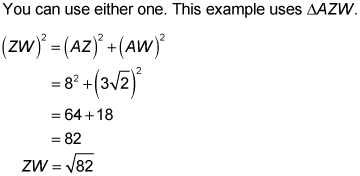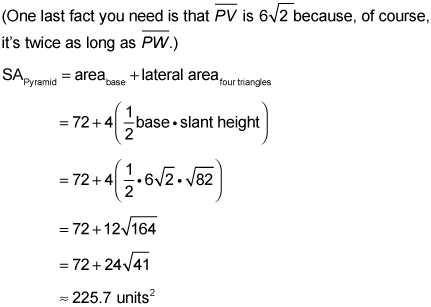The following formula gives you the surface area of a pyramid.
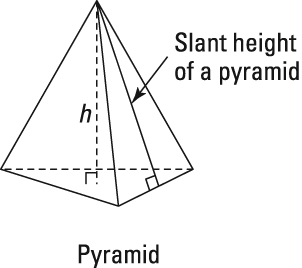
The lateral area of a pyramid is the area of the surface that connects the base to the peak (it's the area of everything but the base). Here's what this means for pyramids:
The lateral area of a pyramid is made up of triangles. Each lateral face of a pyramid is a triangle with an area given by the ordinary area formula,
But you can't use the height of the pyramid for the height of its triangular faces, because the height of the pyramid goes straight down from its peak—it does not go down along the triangular faces. So instead, you use the pyramid's slant height, which is just the ordinary altitude of the triangular faces. (The cursive letter l indicates the slant height.) The above figure shows how height and slant height differ.
Ready for a pyramid problem?
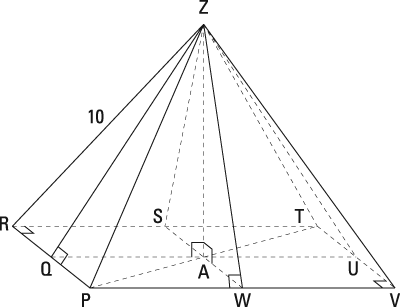
Here's the diagram.
To use the pyramid surface area formula, you need the area of the base and the area of the triangular faces. So, start with the area of the base:
To get the faces, you need the slant height, line ZW.
First, solve triangle PAW. It's a 45-45-90 triangle with a hypotenuse (line PA) that's 6 units long; to get the legs, you divide the hypotenuse by the square root of 2 (or use the Pythagorean Theorem):
Now you can get line ZW by using the Pythagorean Theorem with either of two right triangles, PZW or AZW.
Now you're all set to finish with the surface area formula.
That's a wrap.